Optimization and Multivariate Calculus¶
We will use optimization to motivate the development of multivariate calculus.
Multivariate calculus¶
For a sufficiently smooth scalar function $f: \mathbb{R} \mapsto \mathbb{R}$, we have the second order Taylor approximation:
$$ f(x + \Delta x) \approx f(x) + \Delta x \frac{d}{dx}f(x) + \frac 12 (\Delta x)^2 \frac{d^2}{dx^2}f(x). $$TODO: graph
To generalize to a multivariate function $f: \mathbb{R}^n \mapsto \mathbb{R}$, we need notations:
- Gradient: $$ \nabla f(\mathbf{x}) = \begin{pmatrix} \frac{\partial}{\partial x_1} f(\mathbf{x}) \\ \vdots \\ \frac{\partial}{\partial x_n} f(\mathbf{x}) \end{pmatrix}. $$
- Hessian: $$ H(\mathbf{x}) = \nabla^2 f(\mathbf{x}) = \begin{pmatrix} \frac{\partial^2}{\partial x_1^2} f(\mathbf{x}) & \cdots & \frac{\partial^2}{\partial x_1 \partial x_n} f(\mathbf{x}) \\ \vdots & \ddots & \vdots \\ \frac{\partial^2}{\partial x_n \partial x_1} f(\mathbf{x}) & \cdots & \frac{\partial^2}{\partial x_n^2} f(\mathbf{x}) \end{pmatrix}. $$
Example: TODO.
For a sufficiently smooth multivariate function $f: \mathbb{R}^n \mapsto \mathbb{R}$, we have Taylor approximation:
$$ f(\mathbf{x} + \Delta \mathbf{x}) \approx f(\mathbf{x}) + \nabla f(\mathbf{x})' \Delta \mathbf{x} + \frac 12 \Delta \mathbf{x}' [\nabla^2 f(\mathbf{x})] \Delta \mathbf{x}. $$For a vector function $f: \mathbb{R}^{n} \mapsto \mathbb{R}^m$ $$ f(\mathbf{x}) = \begin{pmatrix} f_1(\mathbf{x}) \\ \vdots \\ f_m(\mathbf{x}) \end{pmatrix}, $$ the $m \times n$ Jacobian matrix is $$ \mathbf{J} = \begin{pmatrix} \nabla f_1' \\ \vdots \\ \nabla f_m' \end{pmatrix} = \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}. $$ The Jacobian is the determant of $\mathbf{J}$ and appears in the multi-dimensional integrals.
Later we will develop chain rule for the vector and matrix functions.
Optimization and optimality conditions¶
Optimization aims to minimize a multivariate function $f: \mathbb{R}^n \mapsto \mathbb{R}$ possibly subject to certain constraints. Possible constrains include
- Linear constraints: $\mathbf{A} \mathbf{x} = \mathbf{b}$.
- Inequality constraints: $\mathbf{x} \ge \mathbf{0}$.
- Integer constraints: Each $x_i$ is either 0 or 1.
Statisticians often talk about maximization, because of the maximum likelihood estimation (MLE). Note maximizing $f$ is same as minimizing $-f$.
For unconstrained optimization of a scalar function $f$, we know
- the necessary condition for a point $x$ to be a local minimum is $\frac{d}{dx} f(x)= 0$.
- a sufficient condition for a strict local minimum is (1) $\frac{d}{dx} f(x) = 0$ and (2) $\frac{d^2}{dx^2} f(x) > 0$.
These are called the optimality conditions.
Similarly for unconstrained optimization of a multivariate function $f: \mathbb{R}^n \mapsto \mathbb{R}$,
- the necessary condition for a point $\mathbf{x}$ to be a local minimum is $$ \nabla f(\mathbf{x}) = \mathbf{0}_n. $$
- a sufficient condition for a strict local minimum is $$ \nabla f(\mathbf{x}) = \mathbf{0}_n $$ and $$ \nabla^2 f(\mathbf{x}) \succ \mathbf{O}_{n \times n}. $$
A body of work in optimization is to generalize these optimality conditions to the constrained case.
Convexity¶
Convexity plays a key role in optimization.
- A convex set $\mathcal{K}$: If $\mathbf{x}, \mathbf{y} \in \mathcal{K}$, then the line from $\mathbf{x}$ to $\mathbf{y}$ $\{\alpha \mathbf{x} + (1 - \alpha) \mathbf{y}: \alpha \in [0, 1]\} \subseteq \mathcal{K}$.
- A convex function $f$: $$ f(\alpha \mathbf{x} + (1 - \alpha) \mathbf{y}) \le \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}) $$ for all $\mathbf{x}, \mathbf{y}$ and $\alpha \in (0, 1)$.
- A strictly convex function satisifies above definition but replacing $\le$ by $<$.
- A convex function $f$ (alternative definition): The set of points on and above the graph of $f$, $\{(\mathbf{x},y): f(\mathbf{x}) \le y\}$, is convex.
- A smooth and convex $f$: $f(\mathbf{x}) \ge f(\mathbf{y}) + \nabla f(\mathbf{y})' (\mathbf{x} - \mathbf{y})$ for all $\mathbf{x}, \mathbf{y}$. The function $f$ sits above its tangent lines.
TODO: A convex function sits between its tangent lines and its chords.
TODO: graph of convex and nonconvex sets/functions.
Examples: $f_1(x) = ax + b$, $f_2(x) = x^2$, and $f_3(x) = \max(f_1(x), f_2(x))$.
Intersection of convex sets is convex.
The maximum of two or more convex functions is always convex.
Proof: Let $f(\mathbf{x}) = \sup_{i \in \mathcal{I}} f_i (\mathbf{x})$. Then $$ f_i(\alpha \mathbf{x} + (1 - \alpha) \mathbf{y}) \le \alpha f_i(\mathbf{x}) + (1 - \alpha) f_i(\mathbf{y}) \le \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}) $$ for all $i \in \mathcal{I}$. Taking supremum over $i$ on the left hand side yields $$ f(\alpha \mathbf{x} + (1 - \alpha) \mathbf{y}) \le \alpha f(\mathbf{x}) + (1 - \alpha) f(\mathbf{y}). $$
Note the minimum of convex functions is usually not convex.
The set of positive (semi)definite matrices is convex.
A twice differentiable function is convex if $\nabla^2 f(\mathbf{x}) \succeq \mathbf{O}_{n \times n}$ at all $\mathbf{x}$. It is strictly convex $\nabla^2 f(\mathbf{x}) \succ \mathbf{O}_{n \times n}$ at all $\mathbf{x}$.
Convexity prevents two local minima. For a convex function, any stationary point with $\nabla f(\mathbf{x}) = \mathbf{0}$ is a global minimum.
Optimality conditions for constrained optimization¶
Example: \begin{eqnarray*} &\text{minimize}& f(x_1,x_2) = x_1^2 + x_2^2 \\ &\text{subject to}& a_1 x_1 + a_2 x_2 = b. \end{eqnarray*} Define the Lagrangian $$ L(x_1, x_2, \lambda) = f(x_1, x_2) + \lambda (a_1 x_1 + a_2 x_2 - b) = x_1^2 + x_2^2 + \lambda (a_1 x_1 + a_2 x_2 - b), $$ where $\lambda$ is the Lagrange multiplier. Solve the equations \begin{eqnarray*} \frac{\partial}{\partial x_1} L &=& 2 x_1 + \lambda a_1 \\ \frac{\partial}{\partial x_2} L &=& 2 x_2 + \lambda a_2 \\ \frac{\partial}{\partial \lambda} L &=& a_1 x_1 + a_2 x_2 - b \end{eqnarray*} to get optimal $x_1$, $x_2$, and $\lambda$: \begin{eqnarray*} x_1^\star &=& \frac{a_1 b}{a_1^2 + a_2^2} \\ x_2^\star &=& \frac{a_2 b}{a_1^2 + a_2^2} \\ \lambda^\star &=& - \frac{2b}{a_1^2 + a_2^2} \end{eqnarray*} with optimal objective value $$ (x_1^\star)^2 + (x_2^\star)^2 = \frac{b^2}{a_1^2 + a_2^2}. $$ We found $-\lambda^\star$ is simply the derivative of the minimum cost with respect to the constraint level $b$ $$ \frac{d}{d b} \left( \frac{b^2}{a_1^2 + a_2^2} \right) = \frac{2b}{a_1^2 + a_2^2} = - \lambda. $$
We generalize above example to the general problem of minimizing a convex quadratic function with linear constraints. For $\mathbf{S} \succ \mathbf{0}$ and $\mathbf{A} \in \mathbb{R}^{n \times m}$, \begin{eqnarray*} &\text{minimize}& \frac 12 \mathbf{x}' \mathbf{S} \mathbf{x} \\ &\text{subject to}& \mathbf{A}' \mathbf{x} = \mathbf{b}. \end{eqnarray*} The Lagrangian function is $$ L(\mathbf{x}, \boldsymbol{\lambda}) = \frac 12 \mathbf{x}' \mathbf{S} \mathbf{x} + \boldsymbol{\lambda}' (\mathbf{A}' \mathbf{x} - \mathbf{b}), $$ where $\boldsymbol{\lambda} \in \mathbb{R}^m$ is the Lagrange multipliers. Solving equations \begin{eqnarray*} \nabla_\mathbf{x} L(\mathbf{x}, \boldsymbol{\lambda}) &=& \mathbf{S} \mathbf{x} + \mathbf{A} \boldsymbol{\lambda} = \mathbf{0}_n \\ \nabla_\boldsymbol{\lambda} L(\mathbf{x}, \boldsymbol{\lambda}) &=& \mathbf{A}' \mathbf{x} - \mathbf{b} = \mathbf{0}_m, \end{eqnarray*} or equivalently $$ \begin{pmatrix} \mathbf{S} & \mathbf{A} \\ \mathbf{A}' & \mathbf{O} \end{pmatrix} \begin{pmatrix} \mathbf{x} \\ \boldsymbol{\lambda} \end{pmatrix} = \begin{pmatrix} \mathbf{0}_n \\ \mathbf{b} \end{pmatrix} \quad \quad (\text{saddle point matrix or KKT matrix}) $$ yields the solution \begin{eqnarray*} \mathbf{x}^\star &=& \mathbf{S}^{-1} \mathbf{A} (\mathbf{A}' \mathbf{S}^{-1} \mathbf{A})^{-1} \mathbf{b} \\ \boldsymbol{\lambda}^\star &=& - (\mathbf{A}' \mathbf{S}^{-1} \mathbf{A})^{-1} \mathbf{b}. \end{eqnarray*} Further calculation shows the minimum cost $$ f^\star = \frac 12 \mathbf{b}' (\mathbf{A}' \mathbf{S}^{-1} \mathbf{A})^{-1} \mathbf{b} $$ and the gradient of cost $$ \nabla_\mathbf{b} f^\star = (\mathbf{A}' \mathbf{S}^{-1} \mathbf{A})^{-1} \mathbf{b} = - \boldsymbol{\lambda}^\star. $$
The saddle point matrix (or KKT matrix) has $n$ positive eigenvalues and $m$ negative eigenvalue. The Lagrangian function is convex in $\mathbf{x}$ and concave in $\boldsymbol{\lambda}$.
Example: MLE of multivariate normal model¶
Let $\mathbf{y}_1, \ldots, \mathbf{y}_n$ be iid samples from a multivariate normal distribution $N(\boldsymbol{\mu}, \boldsymbol{\Omega})$. The log-likelihood is $$ L(\boldsymbol{\mu}, \boldsymbol{\Omega}) = - \frac n2 \log \det \boldsymbol{\Omega} - \frac 12 \sum_{i=1}^n (\mathbf{y}_i - \boldsymbol{\mu})' \boldsymbol{\Omega}^{-1} (\mathbf{y}_i - \boldsymbol{\mu}). $$ We want to maximize $L(\boldsymbol{\mu}, \boldsymbol{\Omega})$ or minimize $$ f(\boldsymbol{\mu}, \boldsymbol{\Omega}) = - L(\boldsymbol{\mu}, \boldsymbol{\Omega}) = \frac n2 \log \det \boldsymbol{\Omega} + \frac 12 \sum_{i=1}^n (\mathbf{y}_i - \boldsymbol{\mu})' \boldsymbol{\Omega}^{-1} (\mathbf{y}_i - \boldsymbol{\mu}). $$ The MLE is achieved by \begin{eqnarray*} \widehat{\boldsymbol{\mu}} &=& \frac{\sum_{i=1}^n \mathbf{y}_i}{n} \\ \widehat{\boldsymbol{\Omega}} &=& \frac{\sum_{i=1}^n (\mathbf{y}_i - \hat{\boldsymbol{\mu}})(\mathbf{y}_i - \hat{\boldsymbol{\mu}})'}{n}. \end{eqnarray*}
TODO: derivation.
Example: MLE of multinomial model¶
Consider a multinomial experiment with $n$ trials and observed outcomes $n_1, \ldots, n_m$ over $m$ categories. The maximum likelihood estimate (MLE) seeks maximizer of likelihood
$$
L(p_1,\ldots,p_m) = \binom{n}{n_1 \cdots n_m} \prod_{i=1}^m p_i^{n_i}.
$$
To minimize the negative log-likelihood
$$
\log L(p_1,\ldots,p_m) = \log \binom{n}{n_1 \cdots n_m} + \sum_{i=1}^m n_i \log p_i
$$
subject to the constraint $p_1 + \cdots + p_m = 1$, we find the statinary point of Lagrangian
$$
L(p_1,\ldots,p_m, \lambda) = - \log \binom{n}{n_1 \cdots n_m} - \sum_{i=1}^m n_i \log p_i + \lambda \left( \sum_{i=1}^m p_i - 1 \right).
$$
Solving
$$
\frac{\partial}{\partial p_i} L = - \frac{n_i}{p_i} + \lambda = 0
$$
gives
$$
\frac{n_i}{p_i} = \lambda.
$$
Combining with the constraint $\sum_i p_i=1$ yields
\begin{eqnarray*}
p_i^\star &=& \frac{n_i}{n}, \quad i=1,\ldots,m, \\
\lambda^\star &=& n.
\end{eqnarray*}
Note the nonnegativity constraint is automatically satisfied.
Newton's method¶
We are looking for a point $\mathbf{x}^\star$ such that $\nabla f(\mathbf{x}^\star) = \mathbf{0}$. Multivariate calculus gives us a principled way to move towards such an $\mathbf{x}^\star$.
Second-order Taylor approximation to a function $f$ at current iterate $\mathbf{x}^{(t)}$ says $$ f(\mathbf{x}^{(t)} + \Delta \mathbf{x}) \approx f(\mathbf{x}^{(t)}) + \nabla f(\mathbf{x}^{(t)})' \Delta \mathbf{x} + \frac 12 \Delta \mathbf{x}' [\nabla^2 f(\mathbf{x}^{(t)})] \Delta \mathbf{x}. $$ Which direction $\Delta \mathbf{x}$ shall we move from $\mathbf{x}^{(t)}$?
Minimizing the quadratic approximation gives the Newton direction $$ \Delta \mathbf{x}_{\text{newton}} = - [\nabla^2 f(\mathbf{x}^{(t)})]^{-1} \nabla f(\mathbf{x}^{(t)}). $$
So the Newton method iterates according to $$ \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} + \Delta \mathbf{x}_{\text{newton}} = \mathbf{x}^{(t)} - [\nabla^2 f(\mathbf{x}^{(t)})]^{-1} \nabla f(\mathbf{x}^{(t)}). $$
Quadratic convergence of Newton's method: $$ \|\mathbf{x}^{(t+1)} - \mathbf{x}^\star\| \le C \|\mathbf{x}^{(t)} - \mathbf{x}^\star\|^2. $$
Example: $f(x) = \frac 13 x^3 - 4x$ with $\nabla f(x) = x^2 - 4$ and $\nabla^2 f(x) = 2x$. Newton's iterates are $$ x^{(t+1)} = x^{(t)} - \frac{x^{(t)2}-4}{2x^{(t)}} = \frac{1}{2} \left( x^{(t)} + \frac{4}{x^{(t)}} \right). $$ Let's start from $x^{(0)}=2.5$.
x = 2.5
for iter in 1:5
x = 0.5 * (x + 4 / x)
@show x, x^3 / 3 - 4x
end
- In practice, the Newton's method may suffer from instability; the iterates may escape into infinities or a local maximum. Two remedies are needed:
- Use a positive definite matrix in the quadratic approximation (automatically satisfied by the Hessian of a convex function).
- Line search (backtracking) to guarantee sufficient drop in the objective function $$ f(\mathbf{x}^{(t)} + s \Delta \mathbf{x}) \le f(\mathbf{x}^{(t)}) - \alpha s \Delta \mathbf{x}' [\nabla^2 f(\mathbf{x}^{(t)})] \Delta \mathbf{x}. $$
Gradient descent¶
If we use the identity matrix as a very crude approximation of the Hessian matrix, we obtain the classical gradient descent, or steepest descent, algorithm: $$ \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} - s^{(t)} \nabla f(\mathbf{x}^{(t)}). $$
Gradient descent algorithm is gaining tremendous of interest in modern, large scale optimization problems, because calculation of Hessian is usually quite expensive.
Example: minimize a bivariate quadratic function: $$ f(x_1, x_2) = \frac 12 (x_1^2 + bx_2^2). $$ Gradient: $$ \nabla f(x_1, x_2) = \begin{pmatrix} x_1 \\ bx_2 \end{pmatrix}. $$ Gradient descent algorithm: \begin{eqnarray*} \begin{pmatrix} x_1^{(t+1)} \\ x_2^{(t+1)} \end{pmatrix} &=& \begin{pmatrix} x_1^{(t)} \\ x_2^{(t)} \end{pmatrix} - s^{(t)} \begin{pmatrix} x_1^{(t)} \\ bx_2^{(t)} \end{pmatrix} \\ &=& \begin{pmatrix} (1 - s^{(t)}) x_1^{(t)} \\ (1 - bs^{(t)})x_2^{(t)} \end{pmatrix}. \end{eqnarray*} What's the optimal step length $s$ (exact line search)? The objective function $$ f(s) = \frac 12 \left[(1-s)^2 x_1^{(t)2} + b(1-bs)^2x_2^{(t)2} \right] $$ is minimized at $$ s^{(t)} = \frac{x_1^{(t)2} + b^2 x_2^{(t)2}}{x_1^{(t)2} + b^3 x_2^{(t)2}}. $$ Let's assume starting point $(x_1^{(0)}, x_2^{(0)}) = (b, 1)$ to simplify analysis. Then $$ s^{(0)} = \frac{b^2 + b^2}{b^2 + b^3} = \frac{2}{b + 1} $$ and $$ \begin{pmatrix} x_1^{(1)} \\ x_2^{(1)} \end{pmatrix} = \begin{pmatrix} \left( \frac{b-1}{b+1} \right) x_1^{(1)} \\ \left( \frac{1-b}{b+1} \right) x_2^{(1)} \end{pmatrix} = \begin{pmatrix} b \left( \frac{b-1}{b+1} \right) \\ \left( \frac{1-b}{b+1} \right) \end{pmatrix}. $$ Continuing this way, we found $$ \begin{pmatrix} x_1^{(t)} \\ x_2^{(t)} \end{pmatrix} = \begin{pmatrix} b \left( \frac{b-1}{b+1} \right)^t \\ \left( \frac{1-b}{b+1} \right)^t \end{pmatrix} $$ and $$ f(x_1^{(t)}, x_2^{(t)}) = \frac 12 (1 + b^2) \left( \frac{b-1}{b+1} \right)^{2t} = \left( \frac{b-1}{b+1} \right)^{2t} f(x_1^{(0)}, x_2^{(0)}). $$
Following graph shows the zig-zagging pattern of the gradient descent iterates:
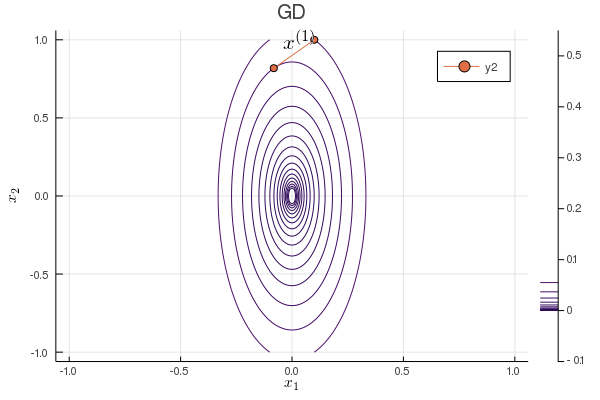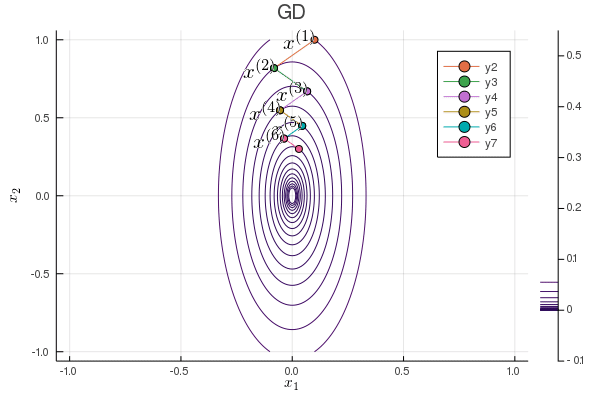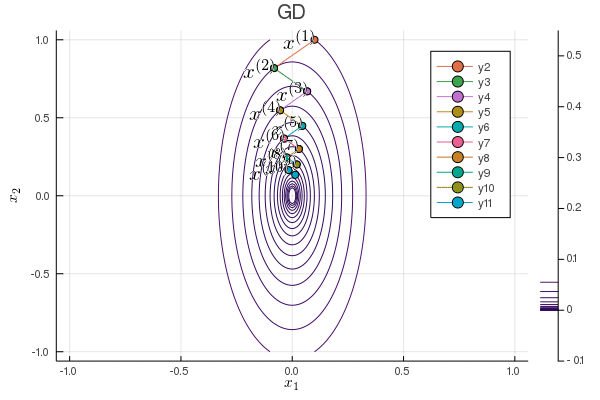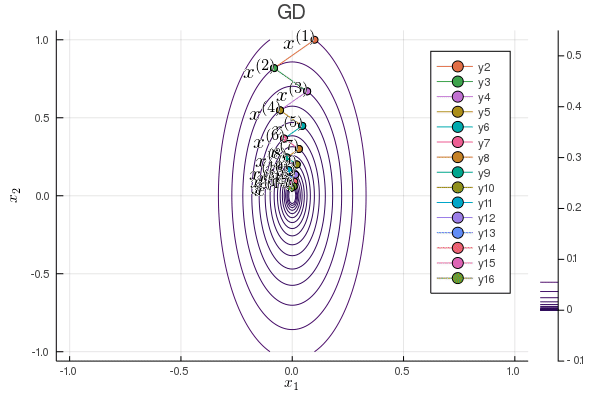
using Plots; gr()
using LaTeXStrings
b = 0.1
f(x1, x2) = 0.5 * (x1^2 + b * x2^2)
s = 2 / (1 + b) # optimal step length
x1, x2 = b, 1.0 # start point
x1iter, x2iter, fiter = [x1], [x2], [f(x1, x2)] # store function values
for iter in 1:15
x1 *= (1 - s)
x2 *= (1 - s * b)
push!(x1iter, x1)
push!(x2iter, x2)
push!(fiter, f(x1, x2))
end
x1 = -1:0.01:1
x2 = -1:0.01:1
X1 = repeat(reshape(x1, 1, :), length(x2), 1)
X2 = repeat(x2, 1, length(x1))
Z = map(f, X1, X2)
p = contour(x1, x2, Z, levels=fiter)
plot(p, xlabel=L"x_1", ylabel=L"x_2", title="GD");
anim = @animate for iter in 1:length(x1iter)-1
Plots.plot!(p, x1iter[iter:iter+1], x2iter[iter:iter+1], shape=:circle)
Plots.annotate!(p, x1iter[iter], x2iter[iter], text(latexstring("x^{($iter)}"), :right))
end
gif(anim, "./gd.gif", fps = 1);
Above analysis can be generalized to a general strongly convex function that satisfies $$ m \mathbf{I}_n \preceq \nabla^2 f(\mathbf{x}) \preceq M \mathbf{I}_n \text{ for all } \mathbf{x} $$ for some constants $M > m > 0$. Or equivalently all eigenvalues of $\nabla^2 f(\mathbf{x})$ are in $[m, M]$.
Theorem: for any strongly convex function $f$, the gradient descent with exact line search satisfies $$ f(\mathbf{x}^{(t+1)}) - f(\mathbf{x}^\star) \le \left( 1 - \frac mM \right) [f(\mathbf{x}^{(t)}) - f(\mathbf{x}^\star)], $$ where $\mathbf{x}^\star$ is the optimum.
In practice, we often perform inexact line search such as backtracking, because exact line search is expensive.
Gradient descent with momentum¶
To mitigate the frustrating zig-zagging of gradient descent, Polyak proposed to add a momentum with coefficient $\beta$ to the gradient. The idea is that a heavy ball rolling downhill has less zig-zagging.
Gradient descent with momentum:
\begin{eqnarray*} \mathbf{x}^{(t+1)} &=& \mathbf{x}^{(t)} - s \mathbf{z}^{(t)} \text{ with } \\ \mathbf{z}^{(t)} &=& \nabla f(\mathbf{x}^{(t)}) + \beta \mathbf{z}^{(t-1)}. \end{eqnarray*}For a quadratic objective function $$ f(\mathbf{x}) = \frac 12 \mathbf{x}' \mathbf{S} \mathbf{x}. $$ The optimal step length $s$ and momentum coefficient $\beta$ are given by (derivation omitted) \begin{eqnarray*} s = \left( \frac{2}{\sqrt{\lambda_{\text{max}}} + \sqrt{\lambda_{\text{min}}}} \right)^2 \\ \beta = \left( \frac{\sqrt{\lambda_{\text{max}}} - \sqrt{\lambda_{\text{min}}}}{\sqrt{\lambda_{\text{max}}} + \sqrt{\lambda_{\text{min}}}} \right)^2, \end{eqnarray*} where $\lambda_{\text{min}}$ and $\lambda_{\text{max}}$ are the minimum and maximum eigenvalues of $\mathbf{S}$.
Back to our 2-dimensional example $f(x_1, x_2) = \frac 12 (x_1^2 + b x_2^2)$. We have $$ s = \left( \frac{2}{1+\sqrt b} \right)^2, \quad \beta = \left( \frac{1 - \sqrt b}{1 + \sqrt b} \right)^2, $$ and $$ f(x_1^{(t)}, x_2^{(t)}) = \left( \frac{1 - \sqrt b}{1 + \sqrt b} \right)^{2t} f(x_1^{(0)}, x_2^{(0)}). $$ The convergence rate improves from $\left( \frac{1 - b}{1 + b} \right)^{2}$ to $\left( \frac{1 - \sqrt b}{1 + \sqrt b} \right)^{2}$.
Following graph shows the iterates of gradient descent with momentum:
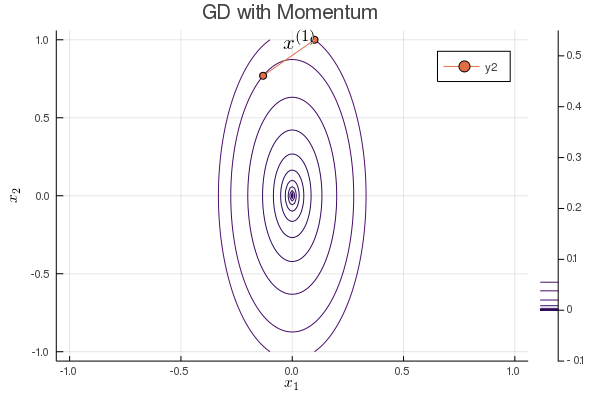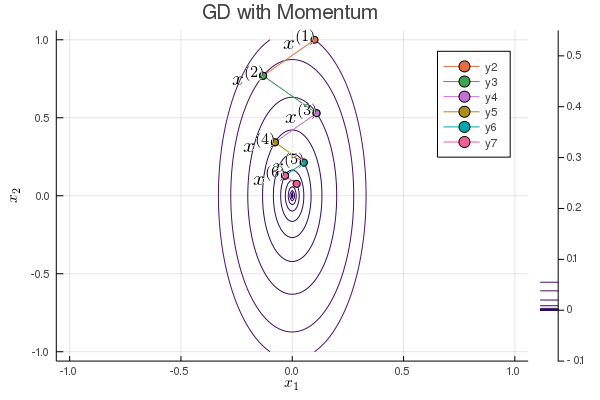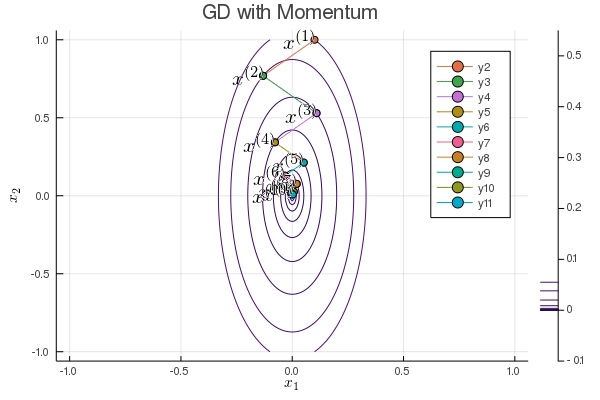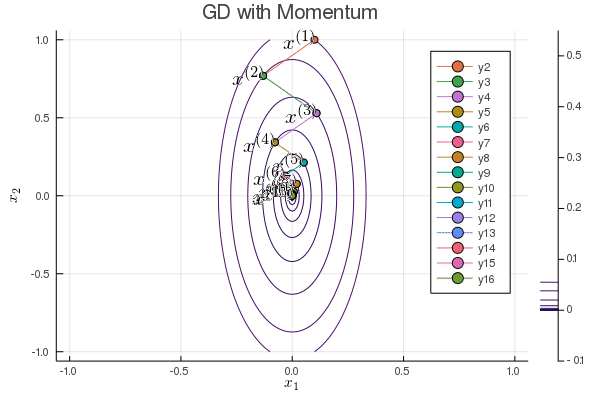
b = 0.1
f(x1, x2) = 0.5 * (x1^2 + b * x2^2)
s = (2 / (1 + sqrt(b)))^2 # optimal step length
β = ((1 - sqrt(b)) / (1 + sqrt(b)))^2 # optimal momentum coefficient
x1, x2 = b, 1.0 # start point
z1, z2 = [0.0, 0.0]
x1iter, x2iter, fiter = [x1], [x2], [f(x1, x2)] # store function values
for iter in 1:15
z1 = x1 + β * z1
z2 = b * x2 + β * z2
x1 -= s * z1
x2 -= s * z2
push!(x1iter, x1)
push!(x2iter, x2)
push!(fiter, f(x1, x2))
end
x1 = -1:0.01:1
x2 = -1:0.01:1
X1 = repeat(reshape(x1, 1, :), length(x2), 1)
X2 = repeat(x2, 1, length(x1))
Z = map(f, X1, X2)
p = contour(x1, x2, Z, levels=fiter)
plot(p, xlabel=L"x_1", ylabel=L"x_2", title="GD with Momentum");
anim = @animate for iter in 1:length(x1iter)-1
Plots.plot!(p, x1iter[iter:iter+1], x2iter[iter:iter+1], shape=:circle)
Plots.annotate!(p, x1iter[iter], x2iter[iter], text(latexstring("x^{($iter)}"), :right))
end
gif(anim, "./gd_momentum.gif", fps = 1);
Nesterov acceleration of gradient descent¶
Yuri Nesterov proposed that, instead of evaluating the gradient $\nabla f$ at current iterate $\mathbf{x}^{(t)}$, we shift the evaluation point to $\mathbf{x}^{(t)} + \gamma (\mathbf{x}^{(t)} - \mathbf{x}^{(t-1)})$.
Nesetrov accelerated gradient descent \begin{eqnarray*} \mathbf{x}^{(t+1)} &=& \mathbf{x}^{(t)} - s \nabla f(\mathbf{y}^{(t)}) \\ \mathbf{y}^{(t+1)} &=& \mathbf{x}^{(t+1)} + \gamma (\mathbf{x}^{(t+1)} - \mathbf{x}^{(t)}). \end{eqnarray*}
For a quadratic objective function $$ f(\mathbf{x}) = \frac 12 \mathbf{x}' \mathbf{S} \mathbf{x}. $$ The optimal step length $s$ and $\gamma$ are given by (derivation omitted) \begin{eqnarray*} s &=& \frac{1}{\lambda_{\text{max}}} \\ \gamma &=& \frac{\sqrt{\lambda_{\text{max}}} - \sqrt{\lambda_{\text{min}}}}{\sqrt{\lambda_{\text{max}}} + \sqrt{\lambda_{\text{min}}}}, \end{eqnarray*} where $\lambda_{\text{min}}$ and $\lambda_{\text{max}}$ are the minimum and maximum eigenvalues of $\mathbf{S}$.
The convergence rate improves from $\left( \frac{1 - b}{1 + b} \right)^{2}$ to $1 - \sqrt b$.
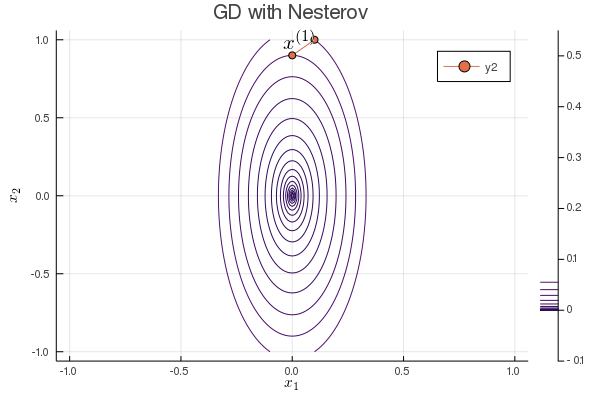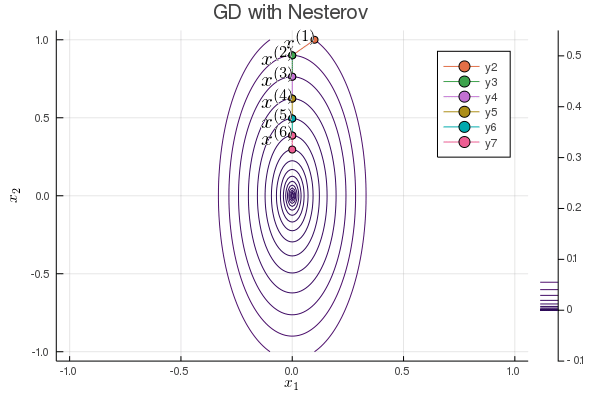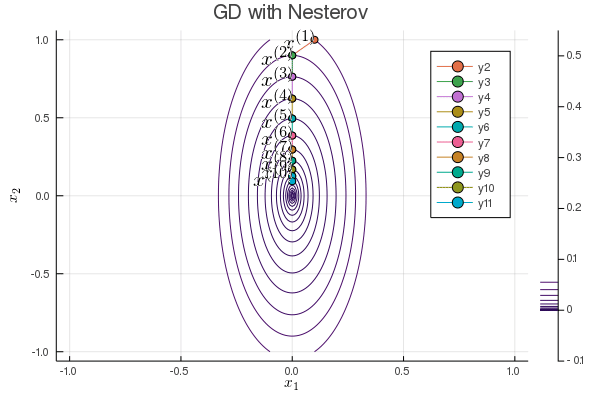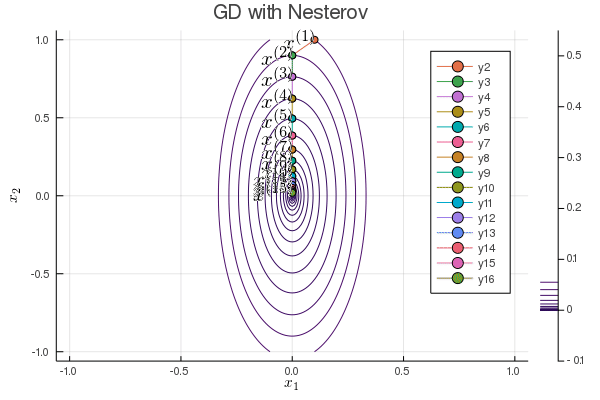
b = 0.1
f(x1, x2) = 0.5 * (x1^2 + b * x2^2)
s = 1.0 # optimal step length
γ = (1 - sqrt(b)) / (1 + sqrt(b)) # optimal Nesterov constant
x1, x2 = b, 1.0 # start point
y1, y2 = x1, x2
x1iter, x2iter, fiter = [x1], [x2], [f(x1, x2)] # store iterates
for iter in 1:15
x1prev, x2prev = x1, x2
x1 = y1 - s * y1
x2 = y2 - s * b * y2
y1 = x1 + γ * (x1 - x1prev)
y2 = x2 + γ * (x2 - x2prev)
push!(x1iter, x1)
push!(x2iter, x2)
push!(fiter, f(x1, x2))
end
x1 = -1:0.01:1
x2 = -1:0.01:1
X1 = repeat(reshape(x1, 1, :), length(x2), 1)
X2 = repeat(x2, 1, length(x1))
Z = map(f, X1, X2)
p = contour(x1, x2, Z, levels=fiter)
plot(p, xlabel=L"x_1", ylabel=L"x_2", title="GD with Nesterov");
anim = @animate for iter in 1:length(x1iter)-1
Plots.plot!(p, x1iter[iter:iter+1], x2iter[iter:iter+1], shape=:circle)
Plots.annotate!(p, x1iter[iter], x2iter[iter], text(latexstring("x^{($iter)}"), :right))
end
gif(anim, "./gd_nesterov.gif", fps = 1);
Stochastic gradient descent¶
In machine learning and statistics, we need to minimize the loss function of training data $$ L(\mathbf{x}) = \frac 1N \sum_{i=1}^N \ell(\mathbf{x}, \mathbf{v}_i), $$ where $\mathbf{x}$ is the parameter to be fitted, $N$ is the training sample size, and $\mathbf{v}_i$ is the $i$-th sample.
For example, in leasts squares problem, we minimize $$ L(\mathbf{x}) = \frac 1N \|\mathbf{b} - \mathbf{A} \mathbf{x}\|^2 = \frac 1N \sum_{i=1}^N (b_i - \mathbf{a}_i' x)^2. $$
Issues of the (classical) gradient descent scheme $$ \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} - s^{(t)} \nabla L(\mathbf{x}). $$ include:
- Evaluating $\nabla L(\mathbf{x}) = \frac 1N \sum_{i=1}^N \nabla \ell(\mathbf{x}, \mathbf{v}_i)$ can be expensive when $N$ is large.
- The solution found by gradient descent does not generalize well on the test data.
The stochastic gradient descent uses only a mini-batch (of size $B$) of the training data at each step:
$$ \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} - s^{(t)} \frac{1}{B} \sum_{i \in \text{mini-batch}} \nabla \ell(\mathbf{x}, \mathbf{v}_i). $$Stochastic gradient descent solves the two issues of gradient descent. It is the workhorse in deep learning.