Determinant (BR Chapter 10)

We review some basic facts about matrix determinant.

• The determinant of a square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$ is $$ \det (\mathbf{A}) = \sum (-1)^{\phi(j_1,\ldots,j_n)} \prod_{i=1}^n a_{ij_i}, $$ where the summation is over all permutation $(j_1, \ldots, j_n)$ of the set of integers $(1,\ldots,n)$ and $\phi(j_1,\ldots,j_n)$ is the number of transposition to change $(1,\ldots,n)$ to $(j_1,\ldots,j_n)$.

• Example $$ \det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = (-1)^{\phi(1,2)} a_{11} a_{22} + (-1)^{\phi(2,1)} a_{12} a_{21} = a_{11} a_{22} - a_{12} a_{21}. $$

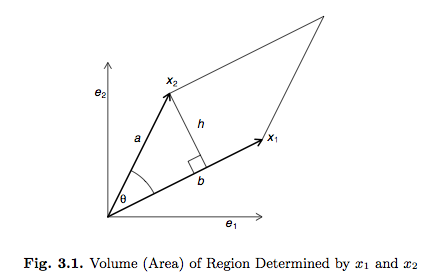
• Interpretation of the (absolute value of) determinant as the volume of the parallelom defined by the columns of the matrix: \begin{eqnarray*} \text{area} &=& bh = \|\mathbf{x}_1\|\|\mathbf{x}_2\| \sin(\theta) \\ &=& \|\mathbf{x}_1\| \|\mathbf{x}_2\| \sqrt{1 - \left( \frac{\langle \mathbf{x}_1, \mathbf{x}_2 \rangle}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|} \right)^2} \\ &=& \sqrt{\|\mathbf{x}_1\|^2 \|\mathbf{x}\|^2 - (\langle \mathbf{x}_1, \mathbf{x}_2\rangle)^2} \\ &=& \sqrt{(x_{11}^2 + x_{12}^2)(x_{21}^2+x_{22}^2) - (x_{11}x_{21} - x_{12}x_{22})^2} \\ &=& |x_{11} x_{22} - x_{12} x_{21}| \\ &=& |\det(\mathbf{X})|. \end{eqnarray*}

• Another interpretation of the determinant is the volume changing factor when operating on a set in $\mathbb{R}^n$. $\text{volume}(f(S)) = |\det(\mathbf{A})| \text{volume}(f(S))$ where $f: \mathbb{R}^n \mapsto \mathbb{R}^n$ is the linear mapping defined by $\mathbf{A}$.

• The determinant of a lower or upper triangular matrix $\mathbf{A}$ is the product of the diagonal elements $\prod_{i=1}^n a_{ii}$.

• Determinant of a singular matrix is 0.

• Determinant of an orthogonal matrix is 1 (rotation) or -1 (reflection).

TODO: visualize a rotation matrix and a reflector.

• $\det(\mathbf{A}') = \det(\mathbf{A})$.

• $\det(\mathbf{A}^{-1}) = 1/\det(\mathbf{A})$.

• $\det(c\mathbf{A}) = c^n \det(\mathbf{A})$.

• $\det(\mathbf{A} \mathbf{B}) = \det(\mathbf{A}) \det(\mathbf{B})$.

• For $\mathbf{A}$ and $\mathbf{D}$ square and nonsingular, \begin{eqnarray*} \det \left( \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{C} & \mathbf{D} \end{pmatrix} \right) = \det (\mathbf{A}) \det (\mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B}) = \det(\mathbf{D}) \det(\mathbf{A} - \mathbf{B} \mathbf{D}^{-1} \mathbf{C}). \end{eqnarray*}

  Proof: Take determinant on the both sides of the matrix identity \begin{eqnarray*} \begin{pmatrix} \mathbf{A} & \mathbf{0} \\ \mathbf{0} & \mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B} \end{pmatrix} = \begin{pmatrix} \mathbf{I} & \mathbf{0} \

  • \mathbf{C} \mathbf{A}^{-1} & \mathbf{I} \end{pmatrix} \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{C} & \mathbf{D} \end{pmatrix} \begin{pmatrix} \mathbf{I} & - \mathbf{A}^{-1} \mathbf{B} \\ \mathbf{0} & \mathbf{I} \end{pmatrix}. \end{eqnarray*}