Orthogonal projections (BR Chapters 7, 8)¶

Highlights In this lecture, we'll show (1) the fundamental theorem of linear algebra:

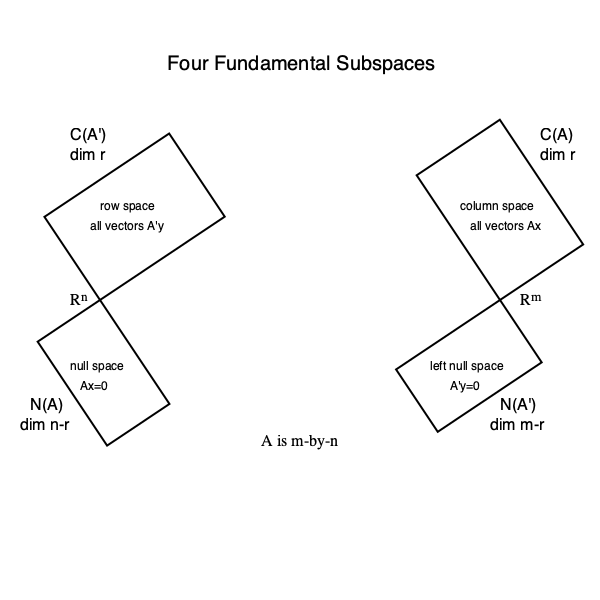
and (2) any symmetric, idempotent matrix $\mathbf{P}$ is the orthogonal projector onto $\mathcal{C}(\mathbf{P})$.

Inner product and orthogonality¶

The inner product between two vectors $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ is defined as $$ \langle \mathbf{x}, \mathbf{y} \rangle = \mathbf{x}' \mathbf{y} = \sum_{i=1}^n x_i y_i. $$
The $\ell_2$ norm or Euclidean norm of a vector $\mathbf{x} \in \mathbb{R}^n$ is $\|\mathbf{x}\| = \sqrt{\langle \mathbf{x}, \mathbf{y} \rangle} = \sqrt{\sum_i x_i^2}$.
Cauchy-Schwarz inequality. Let $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$, then $$ \langle \mathbf{x}, \mathbf{y} \rangle^2 \le \|\mathbf{x}\|^2 \|\mathbf{y}\|^2, $$ with equality holding if and only if $\mathbf{x} = \alpha \mathbf{y}$ for some real number $\alpha$.

Proof: BR p180. Expand $0 \le \|\mathbf{x} - \alpha \mathbf{y}\|^2$.
Triangular inequality. Let $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$. Then $$ \|\mathbf{x} + \mathbf{y}\| \le \|\mathbf{x}\| + \|\mathbf{y}\|. $$

Proof: Use Cauchy-Schwarz.
Angle between vectors. The radian measure of the angle between two non-zero vectors $\mathbf{x}, \mathbf{y}$ is defined to be the number $\theta \in [0,\pi]$ such that $$ \cos \theta = \frac{\langle \mathbf{x}, \mathbf{y} \rangle}{\|\mathbf{x}\| \|\mathbf{y}\|} = \left \langle \frac{\mathbf{x}}{\|\mathbf{x}\|}, \frac{\mathbf{y}}{\|\mathbf{y}\|} \right \rangle = \langle \mathbf{u}_x, \mathbf{u}_y \rangle, $$ where $$ \mathbf{u}_x = \frac{\mathbf{x}}{\|\mathbf{x}\|}, \quad \mathbf{u}_y = \frac{\mathbf{y}}{\|\mathbf{y}\|} $$ are called unit vectors or direction vectors.
Two vectors $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ are orthogonal, denoted as $\mathbf{x} \perp \mathbf{y}$, if $\langle \mathbf{x}, \mathbf{y} \rangle = 0$ or the angle $\theta$ between them is such that $\cos \theta = 0$.
Pythagorean identity. If $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ and $\mathbf{x} \perp \mathbf{y}$, then $$ \|\mathbf{x} + \mathbf{y}\|^2 = \|\mathbf{x}\|^2 + \|\mathbf{y}\|^2. $$
A set of vectors are orthonormal if all vectors are unit vectors and orthogonal to each other.
BR Lemma 7.3. A set of non-zero orthogonal vectors are linearly independent.

Proof: Let $\mathbf{x}_1, \ldots, \mathbf{x}_k$ be a set of orthogonal, non-zero vectors. If $\sum_i \alpha_i \mathbf{x}_i = \mathbf{0}$, then $$ \left \langle \sum_i \alpha_i \mathbf{x}_i, \sum_i \alpha_i \mathbf{x}_i \right \rangle = \sum_i \alpha_i^2 \|\mathbf{x}_i\|^2 = 0. $$ Since $\|\mathbf{x}_i\|^2 > 0$ for all $i$, $\alpha_i=0$ for all $i$. This shows $\mathbf{x}_i$ are linearly independent.

Row rank = column rank: a proof using orthogonality¶

We show that the row rank of a matrix $\mathbf{A} \in \mathbb{R}^{m \times n}$ is equal to its column rank.

Let $r$ be the row rank of $\mathbf{A}$ and $\mathbf{x}_1, \ldots, \mathbf{x}_r \in \mathbb{R}^n$ be a basis of the row space of $\mathbf{A}$.

Lemma: The vectors $\mathbf{A} \mathbf{x}_1, \ldots, \mathbf{A} \mathbf{x}_r$ are linearly independent.

Proof: Suppose $$ \sum_{i=1}^r c_i \mathbf{A} \mathbf{x}_i = \mathbf{A} \sum_{i=1}^r c_i \mathbf{x}_i = \mathbf{A} \mathbf{v} = \mathbf{0}, $$ where $\mathbf{v} = \sum_{i=1}^r c_i \mathbf{x}_i$. $\mathbf{v}$ is a linear combination of vectors in $\mathcal{R}(\mathbf{A})$ so $\mathbf{v} \in \mathcal{R}(\mathbf{A})$. Since $\mathbf{A} \mathbf{v} = \mathbf{0}$, $\mathbf{v}$ is orthogonal to each row of $\mathbf{A}$ thus is orthogonal to all vectors in $\mathcal{R}(\mathbf{A})$, including itself. Thus $\mathbf{v}=\mathbf{0}$ and $c_i$ are zero for all $i$. Thus we have shown $\mathbf{A} \mathbf{x}_1, \ldots, \mathbf{A} \mathbf{x}_r$ are linearly independent.

By the lemma, the column rank of $\mathbf{A}$ must be $\ge r$. Now apply the same argument to $\mathbf{A}'$, we have the column rank of $\mathbf{A}$ is $\le r$.

The lemma also provides a convenient way to produce a basis for the column space given a basis for the row space.

Orthogonal projections¶

An orthocomplement set of a set $\mathcal{X}$ (not necessarily a subspace) in a vector space $\mathcal{S} \subseteq \mathbb{R}^m$ is defined as $$ \mathcal{X}^\perp = \{ \mathbf{u} \in \mathcal{S}: \langle \mathbf{x}, \mathbf{u} \rangle = 0 \text{ for all } \mathbf{x} \in \mathcal{X}\}. $$
TODD: visualize $\mathbb{R}^3 = \text{a plane} \oplus \text{plan}^\perp$.
BR Lemma 7.6. Let $\mathcal{X}$ be a subset (not necessarily a subspace) of a vector space $\mathcal{S}$. Then the following statements are true.
1. If $\mathbf{u} \in \mathcal{X}^\perp$, then $\mathbf{u} \in \text{span}(\mathcal{X})^\perp$.
2. $\mathcal{X}^\perp$ is always a subspace, whether or not $\mathcal{X}$ is a subspace.
3. $\text{span}(\mathcal{X}) \subseteq (\mathcal{X}^\perp)^\perp$ is always true, whether or not $\mathcal{X}$ is a subspace.
  
  Proof of 1: Since $\mathbf{u}$ is orthogonal to vectors in $\mathcal{X}$, it is orthogonal to any linear combination of them.
  Proof of 2: If $\mathbf{u}$ and $\mathbf{v}$ are othogonal to all $\mathbf{x} \in \mathcal{X}$, then $\alpha \mathbf{u} + \mathbf{v}$ is orthogonal to all $\mathbf{x} \in \mathcal{X}$. Thus $\mathcal{X}^\perp$ is closed under axpy operation. Note $\{\mathbf{0}\} \in \mathcal{X}^\perp$ trivially.
  Proof of 3: If $\mathbf{x} \in \mathcal{X}$, then $\mathbf{x} \perp \mathbf{u}$ for any $\mathbf{u} \in \mathcal{X}^\perp$. Thus $\mathbf{x} \in (\mathcal{X}^\perp)^\perp$. Therefore any linear combinations of vectors in $\mathcal{X}$ belongs to $(\mathcal{X}^\perp)^\perp$.
BR Theorem 7.4. Direct sum theorem for orthocomplementary subspaces. Let $\mathcal{S}$ be a subspace of a vector space $\mathcal{V}$ with $\text{dim}(\mathcal{V}) = m$. Then the following statements are true.
1. Every vector $\mathbf{y} \in \mathcal{V}$ can be expressed as $\mathbf{y} = \mathbf{u} + \mathbf{v}$, where $\mathbf{u} \in \mathcal{S}$ and $\mathbf{v} \in \mathcal{S}^\perp$.
2. $\mathcal{S} \cap \mathcal{S}^\perp = \{\mathbf{0}\}$ (essentially disjoint).
3. $\mathcal{V} = \mathcal{S} \oplus \mathcal{S}^\perp$.
4. $m = \text{dim}(\mathcal{S}) + \text{dim}(\mathcal{S}^\perp)$.
  By the uniqueness of decomposition for direct sum, we know the expression of $\mathbf{y} = \mathbf{u} + \mathbf{v}$ is also unique.
  
  Proof of 1: Let $\mathbf{z}_1, \ldots, \mathbf{z}_r$ be an orthonormal basis of $\mathcal{S}$, e.g., by applying Gram-Schmidt to a basis of $\mathcal{S}$. And let $\mathbf{z}_{r+1}, \ldots, \mathbf{z}_m$ be an orthonormal basis of $\mathbf{S}^\perp$. Then $$ \mathbf{y} = \sum_{i=1}^r \langle \mathbf{y}, \mathbf{z}_i \rangle \mathbf{z}_i + \sum_{i=r+1}^m \langle \mathbf{y}, \mathbf{z}_i \rangle \mathbf{z}_i, $$ where the first sum belongs to $\mathcal{S}$ and the second to $\mathcal{S}^\perp$.
  Proof of 2: Suppose $\mathbf{x} \in \mathcal{S} \cap \mathcal{S}^\perp$, then $\mathbf{x} \perp \mathbf{x}$, i.e., $\langle \mathbf{x}, \mathbf{x} \rangle = 0$. Therefore $\mathbf{x} = \mathbf{0}$.
  Proof of 3: Statement 1 says $\mathcal{V} = \mathcal{S} + \mathcal{S}^\perp$. Statement 2 says $\mathcal{S}$ and $\mathcal{S}^\perp$ are essentially disjoint. Thus $\mathcal{V} = \mathcal{S} \oplus \mathcal{S}^\perp$.
  Proof of 4: Follows from essential disjointness between $\mathcal{S}$ and $\mathcal{S}^\perp$.
Some facts:
1. If $\mathcal{S}$ is a subspace of $\mathcal{V}$, then $(\mathcal{S}^\perp)^\perp = \mathcal{S}$.
2. If $\mathcal{S}_1 \subseteq \mathcal{S}_2$ are subsets of $\mathcal{V}$, then $\mathcal{S}_1^\perp \supseteq \mathcal{S}_2^\perp$.
3. If $\mathcal{S}_1 = \mathcal{S}_2$ are two subsets of $\mathcal{V}$, then $\mathcal{S}_1^\perp = \mathcal{S}_2^\perp$.
4. If $\mathcal{S}_1$ and $\mathcal{S}_2$ are two subspaces in $\mathcal{V}$, then $(\mathcal{S}_1 + \mathcal{S}_2)^\perp = \mathcal{S}_1^\perp \cap \mathcal{S}_2^\perp$ and $(\mathcal{S}_1 \cap \mathcal{S}_2)^\perp = \mathcal{S}_1^\perp + \mathcal{S}_2^\perp$.
  
  See BR p198-199 for proofs.

The fundamental theorem of linear algebra¶

BR Theorem 7.5. Let $\mathbf{A} \in \mathbb{R}^{m \times n}$. Then
1. $\mathcal{C}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}')$ and $\mathbb{R}^m = \mathcal{C}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A}')$.
2. $\mathcal{C}(\mathbf{A}) = \mathcal{N}(\mathbf{A}')^\perp$.
3. $\mathcal{N}(\mathbf{A})^\perp = \mathcal{C}(\mathbf{A}')$ and $\mathbb{R}^n = \mathcal{N}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A}')$.
  
  Proof of 1: To show $\mathcal{C}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}')$, \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}') \\ &\Leftrightarrow& \mathbf{A}' \mathbf{x} = \mathbf{0} \\ &\Leftrightarrow& \mathbf{x} \text{ is orthogonal to columns of } \mathbf{A} \\ &\Leftrightarrow& \mathbf{x} \in \mathcal{C}(\mathbf{A})^\perp. \end{eqnarray*} Then, by Part 3 of Theorem 7.4, $\mathbb{R}^m = \mathcal{C}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A})^\perp = \mathcal{C}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A}')$.
  
  Proof of 2: Since $\mathcal{C}(\mathbf{A})$ is a subspace, $(\mathcal{C}(\mathbf{A})^\perp)^\perp = \mathcal{N}(\mathbf{A}')^\perp$.
  
  Proof of 3: Applying part 2 to $\mathbf{A}'$, we have $$ \mathcal{C}(\mathbf{A}') = \mathcal{N}((\mathbf{A}')')^\perp = \mathcal{N}(\mathbf{A})^\perp $$ and $$ \mathbb{R}^n = \mathcal{N}(\mathbf{A}) \oplus \mathcal{N}(\mathbf{A})^\perp = \mathcal{N}(\mathbf{A}) \oplus \mathcal{C}(\mathbf{A}'). $$

Orthogonal matrix¶

BR Theorem 8.1. Let $\mathbf{Q} \in \mathbb{R}^{n \times n}$. The following statements are equivalent:
1. The columns of $\mathbf{Q}$ are orthonormal vectors.
2. $\mathbf{Q}'\mathbf{Q} = \mathbf{I} = \mathbf{Q} \mathbf{Q}'$.
3. The rows of $\mathbf{Q}$ are orthonormal vectors.
  
  Proof: We show $1 \Rightarrow 2 \Rightarrow 3 \Rightarrow 1$.
  
  Proof of $1 \Rightarrow 2$: Let $\mathbf{Q} = (\mathbf{q}_1 : \cdots : \mathbf{q}_n)$. Orthonormality of $\mathbf{q}_i$ shows $\mathbf{Q}' \mathbf{Q} = \mathbf{I}$. Also $\mathbf{q}_i$ are linearly independent thus $\mathbf{Q}$ is non-singular. Thus $\mathbf{Q}^{-1} = \mathbf{Q}'$ and $\mathbf{Q} \mathbf{Q}' = \mathbf{Q} \mathbf{Q}^{-1} = \mathbf{I}$.
  
  Proof of $2 \Rightarrow 3$: $\mathbf{Q} \mathbf{Q}' = \mathbf{I}$ shows that the rows of $\mathbf{Q}$ are orthonormal.
  
  Proof of $3 \Rightarrow 1$: Statement 3 says columns of $\mathbf{Q}'$ are orthonormal. We have shown $1 \Rightarrow 2 \Rightarrow 3$. Thus we know rows of $\mathbf{Q}'$ are orthonormal, i.e., columns of $\mathbf{Q}$ are orthonormal.
BR Definition 8.1. Any square matrix $\mathbf{Q} \in \mathbb{R}^{n \times n}$ satisfying $\mathbf{Q} \mathbf{Q}' = \mathbf{Q}' \mathbf{Q} = \mathbf{I}$ is called an orthogonal matrix.
In other words, columns or rows of $\mathbf{Q}$ are orthonormal.
Note for a rectangular matrix $\mathbf{Q} \in \mathbb{R}^{m \times n}$, $m > n$, with orthonormal columns, we have $\mathbf{Q}' \mathbf{Q} = \mathbf{I}_n$ but $\mathbf{Q} \mathbf{Q}' \ne \mathbf{I}_m$.
Any orthogonal matrix is full rank. And its inverse is its transpose.
Examples of orthogonal matrix: $\mathbf{I}$, Householder matrix $\mathbf{H} = \mathbf{I} - 2 \mathbf{u} \mathbf{u}'$ with $\|\mathbf{u}\|=1$, Jacobi matrix.
More example: Hadamard matrix \begin{eqnarray*} \mathbf{H}_2 &=& \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \\ \mathbf{H}_4 &=& \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & 1 \\ 1 & -1 & -1 & 1 \end{pmatrix} \\ \mathbf{H}_8 &=& \begin{pmatrix} \mathbf{H}_4 & \mathbf{H}_4 \\ \mathbf{H}_4 & -\mathbf{H}_4 \end{pmatrix}. \end{eqnarray*} Are these orthogonal matrices?

Hadamard conjecture proposes that there is a $\pm 1$ matrix with orthogonal columns whenever 4 divides $n$. Wikipedia says $n=668$ is the smallest of those sizes without a known Hadamard matrix.
Orthogonal matrix preserves length and angle. If $\mathbf{Q} \in \mathbb{R}^{n \times n}$ is an orthgonal matrix, then
1. $\|\mathbf{Q} \mathbf{x}\| = \|\mathbf{x}\|$ for any $\mathbf{x} \in \mathbb{R}^n$.
2. $\langle \mathbf{Q} \mathbf{x}, \mathbf{Q} \mathbf{y} \rangle = \langle \mathbf{x}, \mathbf{y} \rangle$ for any $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$.
If $\mathbf{Q}_1, \ldots, \mathbf{Q}_k$ are othgononal matrices, then the product $\mathbf{Q} = \mathbf{Q}_1 \cdots \mathbf{Q}_k$ is orthogonal.

Orthogonal projection¶

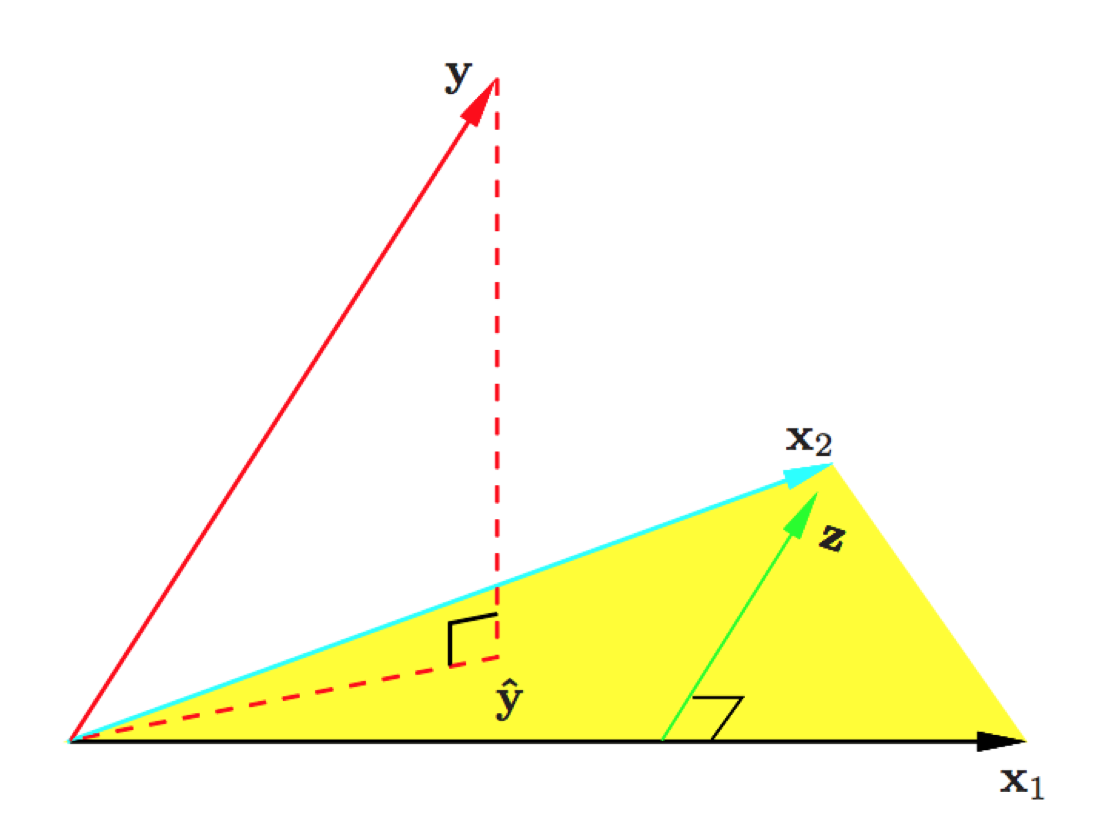
BR Definition 8.2. If $\mathcal{S}$ is a subspace of some vector space $\mathcal{V}$ and $\mathbf{y} \in \mathcal{V}$, then the projection of $\mathbf{y}$ into $\mathcal{S}$ along $\mathcal{S}^\perp$ is called the orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$.
BR Theorem 8.3. The closest point theorem. Let $\mathcal{S}$ be a subspace of some vector space $\mathcal{V}$ and $\mathbf{y} \in \mathcal{V}$. The orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$ is the unique point in $\mathbf{S}$ that is closest to $\mathbf{y}$. In other words, if $\mathbf{u}$ is the orthogonal projection of $\mathbf{y}$ into $\mathcal{S}$, then $$ \|\mathbf{y} - \mathbf{u}\|^2 \le \|\mathbf{y} - \mathbf{w}\|^2 \text{ for all } \mathbf{w} \in \mathcal{S}, $$ with equality holding only when $\mathbf{w} = \mathbf{u}$.

Proof: Picture.
BR Definition 8.3. Let $\mathbb{R}^n = \mathcal{S} \oplus \mathcal{S}^\perp$. A square matrix $\mathbf{P}_{\mathcal{S}}$ is called the orthogonal porjector into $\mathcal{S}$ if, for every $\mathbf{y} \in \mathbb{R}^n$, $\mathbf{P}_{\mathcal{S}} \mathbf{y}$ is the projection of $\mathbf{y}$ into $\mathcal{S}$ along $\mathcal{S}^\perp$.
For a matrix $\mathbf{X}$, the orthogonal projector onto $\mathcal{C}(\mathbf{X})$ is written as $\mathbf{P}_{\mathbf{X}}$.

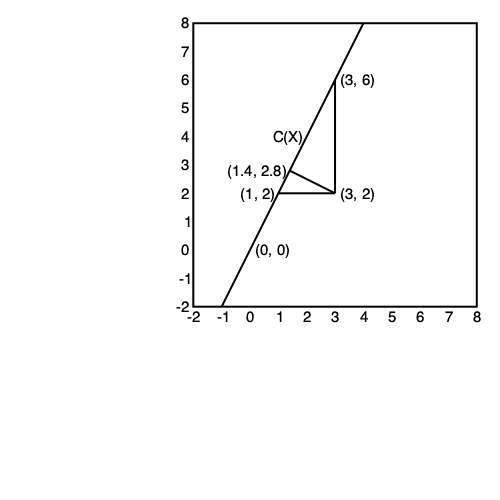
BR Theorem 8.4. Let $\mathbf{y} \in \mathbb{R}^n$ and $\mathbf{X} \in \mathbb{R}^{n \times p}$.
1. The orthogonal projector of $\mathbf{y}$ into $\mathcal{C}(\mathbf{X})$ is given by $\mathbf{u} = \mathbf{X} \boldsymbol{\beta}$, where $\mathbf{\beta}$ satisfies the normal equation $$ \mathbf{X}' \mathbf{X} \boldsymbol{\beta} = \mathbf{X}' \mathbf{y}. $$ Therefore, $$ \mathbf{P}_{\mathbf{X}} \mathbf{y} = \mathbf{X} (\mathbf{X}' \mathbf{X})^- \mathbf{X}' \mathbf{y}. $$ for any generalized inverse $(\mathbf{X}' \mathbf{X})^-$.
2. If $\mathbf{X}$ has full column rank, then the orthogonal projector into $\mathcal{C}(\mathbf{X})$ is given by $$ \mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'. $$
  
  Proof of 1: Since the projection of $\mathbf{y}$ into $\mathcal{C}(\mathbf{X})$ lives in $\mathcal{C}(\mathbf{X})$, thus can be written as $\mathbf{u} = \mathbf{X} \boldsymbol{\beta}$ for some $\boldsymbol{\beta} \in \mathbb{R}^p$. Furthermore, $\mathbf{v} = \mathbf{y} - \mathbf{X} \boldsymbol{\beta} \in \mathcal{C}(\mathbf{X})^\perp$ thus is orthogonal to any vectors in $\mathcal{C}(\mathbf{X})$ including the columns of $\mathbf{X}$. Thus $$ \mathbf{X}' (\mathbf{y} - \mathbf{X} \boldsymbol{\beta}) = \mathbf{0}, $$ or equivalently, $$ \mathbf{X}' \mathbf{X} \boldsymbol{\beta} = \mathbf{X}' \mathbf{y}. $$
  
  Proof of 2: If $\mathbf{X}$ has full column rank, $\mathbf{X}' \mathbf{X}$ is non-singular and the solution to the normal equation is uniquely determined by $\boldsymbol{\beta} = (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{y}$, and the orthogonal projection is $\mathbf{u} = \mathbf{X} \boldsymbol{\beta} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{y}$.
BR Lemma 8.4. Uniqueness of orthogonal projector. Let $\mathbf{A}, \mathbf{B} \in \mathbb{R}^{n \times p}$, both of full column rank and $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{B})$. Then $\mathbf{P}_{\mathbf{A}} = \mathbf{P}_{\mathbf{B}}$.

Proof: Since $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{B})$, there exists a non-singular $\mathbf{C} \in \mathbb{R}^{p \times p}$ such that $\mathbf{A} = \mathbf{B} \mathbf{C}$. Then \begin{eqnarray*} \mathbf{P}_{\mathbf{A}} &=& \mathbf{A} (\mathbf{A}' \mathbf{A})^{-1} \mathbf{A}' \\ &=& \mathbf{B} \mathbf{C} (\mathbf{C}' \mathbf{B}' \mathbf{B} \mathbf{C})^{-1} \mathbf{C}' \mathbf{B}' \\ &=& \mathbf{B} \mathbf{C} \mathbf{C}^{-1} (\mathbf{B}' \mathbf{B})^{-1} (\mathbf{C}')^{-1} \mathbf{C}' \mathbf{B}' \\ &=& \mathbf{B} (\mathbf{B}' \mathbf{B})^{-1} \mathbf{B}' \\ &=& \mathbf{P}_{\mathbf{B}}. \end{eqnarray*}
BR Theorem 8.5. Let $\mathbf{P}_\mathbf{X}$ be the orthogonal projector into $\mathcal{C}(\mathbf{X})$, where $\mathbf{X} \in \mathbb{R}^{n \times p}$ has full column rank. Following statements are true.
1. $\mathbf{P}_\mathbf{X}$ and $\mathbf{I} - \mathbf{P}_\mathbf{X}$ are both symmetric and idemponent.
2. $\mathbf{P}_\mathbf{X} \mathbf{X} = \mathbf{X}$ and $(\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{X} = \mathbf{O}$.
3. $\mathcal{C}(\mathbf{X}) = \mathcal{C}(\mathbf{P}_\mathbf{X})$ and $\text{rank}(\mathbf{P}_\mathbf{X}) = \text{rank}(\mathbf{X}) = p$.
4. $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) = \mathcal{N}(\mathbf{X}') = \mathcal{C}(\mathbf{X})^\perp$.
5. $\mathbf{I} - \mathbf{P}_\mathbf{X}$ is the orthogonal projector into $\mathcal{N}(\mathbf{X}')$ (or $\mathcal{C}(\mathbf{X})^\perp)$.
  
  Proof of 1: Check directly using $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$.
  
  Proof of 2: Check directly using $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$.
  
  Proof of 3: Since $\mathbf{P}_{\mathbf{X}} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}'$, $$ \mathcal{C}(\mathbf{P}_\mathbf{X}) \subseteq \mathcal{C}(\mathbf{X}) = \mathcal{C}(\mathbf{P}_\mathbf{X} \mathbf{X}) \subseteq \mathcal{C}(\mathbf{P}_\mathbf{X}). $$
  
  Proof of 4: The second equality is simply the fundamental theorem of linear algebra. For the first equality, first we show $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \subseteq \mathcal{N}(\mathbf{X}')$: \begin{eqnarray*} & & \mathbf{u} \in \mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \\ &\Rightarrow& \mathbf{u} = (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{v} \text{ for some } \mathbf{v} \\ &\Rightarrow& \mathbf{X}' \mathbf{u} = [(\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{X}]' \mathbf{v} = \mathbf{O} \mathbf{v} = \mathbf{0} \\ &\Rightarrow& \mathbf{u} \in \mathcal{N}(\mathbf{X}'). \end{eqnarray*} To show the other direction $\mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}) \supseteq \mathcal{N}(\mathbf{X}')$, \begin{eqnarray*} & & \mathbf{u} \in \mathcal{N}(\mathbf{X}') \\ &\Rightarrow& \mathbf{X}' \mathbf{u} = \mathbf{0} \\ &\Rightarrow& \mathbf{P}_\mathbf{X} \mathbf{u} = \mathbf{X} (\mathbf{X}' \mathbf{X})^{-1} \mathbf{X}' \mathbf{u} = \mathbf{0} \\ &\Rightarrow& \mathbf{u} = \mathbf{u} - \mathbf{P}_\mathbf{X} \mathbf{u} = (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{u} \\ &\Rightarrow& \mathbf{u} \in \mathcal{C}(\mathbf{I} - \mathbf{P}_\mathbf{X}). \end{eqnarray*}
  
  Proof of 5: For any $\mathbf{y} \in \mathbb{R}^n$, write $\mathbf{y} = \mathbf{P}_\mathbf{X} \mathbf{y} + (\mathbf{I} - \mathbf{P}_\mathbf{X}) \mathbf{y}$.