Rank and nullity (BR Chapter 5)

Highlights: In this lecture we will show some most important results on the rank of a matrix:

  1. column rank = row rank.
  2. Matrix multiplication can only decrease the rank:
    $\text{rank}(\mathbf{A} \mathbf{B}) \le \text{rank}(\mathbf{A})$
    $\text{rank}(\mathbf{A} \mathbf{B}) \le \text{rank}(\mathbf{B})$.
    Two special cases: (1) $\text{rank}(\mathbf{A} \mathbf{B}) = \text{rank}(\mathbf{A})$ if $\mathbf{B}$ has full row rank. (2) $\text{rank}(\mathbf{A}' \mathbf{A}) = \text{rank}(\mathbf{A})$ for any $\mathbf{A}$.
  3. $\text{rank}(\mathbf{A} + \mathbf{B}) \le \text{rank}(\mathbf{B}) + \text{rank}(\mathbf{B})$.
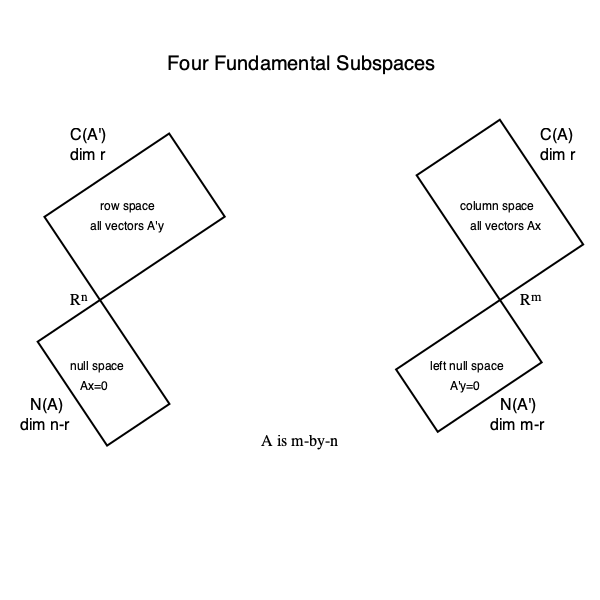
  4. Rank-nullity theorem: For any $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\text{rank}(\mathbf{A}) + \text{nullity}(\mathbf{A}) = n$.
  5. Fundamental theorem of ranks: $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}') = \text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{A}')$.

In [9]:
using LinearAlgebra, RDatasets, StatsModels
In [10]:
# the famous Fisher's Iris data
# <https://en.wikipedia.org/wiki/Iris_flower_data_set>
iris = dataset("datasets", "iris")
Out[10]:

150 rows × 5 columns

SepalLengthSepalWidthPetalLengthPetalWidthSpecies
Float64Float64Float64Float64Categorical…
15.13.51.40.2setosa
24.93.01.40.2setosa
34.73.21.30.2setosa
44.63.11.50.2setosa
55.03.61.40.2setosa
65.43.91.70.4setosa
74.63.41.40.3setosa
85.03.41.50.2setosa
94.42.91.40.2setosa
104.93.11.50.1setosa
115.43.71.50.2setosa
124.83.41.60.2setosa
134.83.01.40.1setosa
144.33.01.10.1setosa
155.84.01.20.2setosa
165.74.41.50.4setosa
175.43.91.30.4setosa
185.13.51.40.3setosa
195.73.81.70.3setosa
205.13.81.50.3setosa
215.43.41.70.2setosa
225.13.71.50.4setosa
234.63.61.00.2setosa
245.13.31.70.5setosa
254.83.41.90.2setosa
265.03.01.60.2setosa
275.03.41.60.4setosa
285.23.51.50.2setosa
295.23.41.40.2setosa
304.73.21.60.2setosa
⋮⋮⋮⋮⋮⋮
In [11]:
# use full dummy coding (one-hot coding) for categorical variable Species
X = ModelMatrix(ModelFrame(
    @formula(1 ~ 1 + SepalLength + SepalWidth + PetalLength + PetalWidth + Species), 
    iris,
    contrasts = Dict(:Species => StatsModels.FullDummyCoding()))).m
Out[11]:
150×8 Array{Float64,2}:
 1.0  5.1  3.5  1.4  0.2  1.0  0.0  0.0
 1.0  4.9  3.0  1.4  0.2  1.0  0.0  0.0
 1.0  4.7  3.2  1.3  0.2  1.0  0.0  0.0
 1.0  4.6  3.1  1.5  0.2  1.0  0.0  0.0
 1.0  5.0  3.6  1.4  0.2  1.0  0.0  0.0
 1.0  5.4  3.9  1.7  0.4  1.0  0.0  0.0
 1.0  4.6  3.4  1.4  0.3  1.0  0.0  0.0
 1.0  5.0  3.4  1.5  0.2  1.0  0.0  0.0
 1.0  4.4  2.9  1.4  0.2  1.0  0.0  0.0
 1.0  4.9  3.1  1.5  0.1  1.0  0.0  0.0
 1.0  5.4  3.7  1.5  0.2  1.0  0.0  0.0
 1.0  4.8  3.4  1.6  0.2  1.0  0.0  0.0
 1.0  4.8  3.0  1.4  0.1  1.0  0.0  0.0
 ⋮                        ⋮            
 1.0  6.0  3.0  4.8  1.8  0.0  0.0  1.0
 1.0  6.9  3.1  5.4  2.1  0.0  0.0  1.0
 1.0  6.7  3.1  5.6  2.4  0.0  0.0  1.0
 1.0  6.9  3.1  5.1  2.3  0.0  0.0  1.0
 1.0  5.8  2.7  5.1  1.9  0.0  0.0  1.0
 1.0  6.8  3.2  5.9  2.3  0.0  0.0  1.0
 1.0  6.7  3.3  5.7  2.5  0.0  0.0  1.0
 1.0  6.7  3.0  5.2  2.3  0.0  0.0  1.0
 1.0  6.3  2.5  5.0  1.9  0.0  0.0  1.0
 1.0  6.5  3.0  5.2  2.0  0.0  0.0  1.0
 1.0  6.2  3.4  5.4  2.3  0.0  0.0  1.0
 1.0  5.9  3.0  5.1  1.8  0.0  0.0  1.0
In [12]:
@show size(X)
@show rank(X)
@show rank(X')
@show rank(X' * X)
@show rank(X * X');

size(X) = (150, 8)
rank(X) = 7
rank(X') = 7
rank(X' * X) = 7
rank(X * X') = 7
In [13]:
# only one basis vector in N(X)
nullspace(X)
Out[13]:
8×1 Array{Float64,2}:
 -0.5                   
 -8.326672684688674e-17 
 -1.9081958235744878e-16
  1.1796119636642288e-16
  2.1510571102112408e-16
  0.5000000000000002    
  0.4999999999999998    
  0.49999999999999956

Rank

Let $\mathbf{A}$ be an $m \times n$ matrix \begin{eqnarray*} \mathbf{A} = \begin{pmatrix} \mid & & \mid \\ \mathbf{a}_1 & \ldots & \mathbf{a}_n \\ \mid & & \mid \end{pmatrix}. \end{eqnarray*}

  • The column rank of $\mathbf{A}$ is the maximum number of linearly independent columns of $\mathbf{A}$.

    In other words, column rank of $\mathbf{A}$ is $\text{dim}(\mathcal{C}(\mathbf{A}))$.

  • The row rank of $\mathbf{A}$ is the maximum number of linearly independent rows of $\mathbf{A}$.

    In other words, row rank of $\mathbf{A}$ is $\text{dim}(\mathcal{R}(\mathbf{A})) = \text{dim}(\mathcal{C}(\mathbf{A}'))$.

  • BR Theorem 4.17. For any $m \times n$ matrix $\mathbf{A}$, its column rank is equal to the row rank, which we shall call the rank of $\mathbf{A}$.

    Our text book BR uses notation $\rho(\mathbf{A})$ to denote the rank of a matrix $\mathbf{A}$.

    Proof: Let $r$ be the row rank of $\mathbf{A}$ and $c$ be the column rank of $\mathbf{A}$. We show $r=c$ by showing $c \le r$ and $c \ge r$.
    Since $\mathbf{A}$ has row rank $r$, we can permute the rows of $\mathbf{A}$ to be
    $$ \begin{pmatrix} \mathbf{A}_1 \\ \mathbf{A}_2 \end{pmatrix} = \begin{pmatrix} \mathbf{A}_1 \\ \mathbf{B} \mathbf{A}_1 \end{pmatrix}, $$ where $\mathbf{A}_1 \in \mathbb{R}^{r \times n}$ has $r$ independent rows and $\mathbf{A}_2 = \mathbf{B} \mathbf{A}_1 \in \mathbb{R}^{(m-r) \times n}$ for some matrix $\mathbf{B}$. Note row permutation does not change the row rank or column rank. Then \begin{eqnarray*} & & \begin{pmatrix} \mathbf{A}_1 \\ \mathbf{B} \mathbf{A}_1 \end{pmatrix} \mathbf{x} = \mathbf{0}_m \\ &\Leftrightarrow& \begin{pmatrix} \mathbf{A}_1 \mathbf{x} \\ \mathbf{B} \mathbf{A}_1 \mathbf{x} \end{pmatrix} = \mathbf{0}_m \\ &\Leftrightarrow& \mathbf{A}_1 \mathbf{x} = \mathbf{0}_r. \end{eqnarray*} This says that take any set of linearly independent columns in $\mathbf{A}$, the corresponding columns in $\mathbf{A}_1$ are linearly independent as well. Therefore the column rank $c$ of $\mathbf{A}$ is less than or equal to the maximum number of linearly independent columns of $\mathbf{A}_1$, which is less than or equal to $r$ by the independence-dimensionality inequality. This way we have shown $c \le r$.
    To show the other direction $c \ge r$, we apply above result to the transpose $\mathbf{A}'$.

  • For any $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\text{rank}(\mathbf{A}) \le \min \{m, n\}$.

In [14]:
@show size(X)
@show rank(X)

size(X) = (150, 8)
rank(X) = 7
Out[14]:
7

  • For $\mathbf{A} \in \mathbb{R}^{m \times n}$, we say $\mathbf{A}$ is full rank if $\text{rank}(\mathbf{A}) = \min \{m, n\}$.

    It is full row rank if $\text{rank}(\mathbf{A}) = m$.

    It is full column rank if $\text{rank}(\mathbf{A}) = n$.

  • A square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$ is singular if $\text{rank}(\mathbf{A}) < n$ and non-singular or invertible if $\text{rank}(\mathbf{A}) = n$.

  • Example: The identity matrix $$ \mathbf{I} = \begin{pmatrix} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{pmatrix} $$ is full rank.

Effects of matrix multiplication on rank

  • BR Lemma 5.1. $\text{rank}(\mathbf{A}\mathbf{B}) \le \min \{\text{rank}(\mathbf{A}), \text{rank}(\mathbf{B})\}$. In words, matrix multiplication can only decrease the rank.

    Proof: Because $\mathcal{C}(\mathbf{A}\mathbf{B}) \subseteq \mathcal{C}(\mathbf{A})$ (why?), we have $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{A})$ by monotonicity of dimension. Similary, because the row space of $\mathbf{A}\mathbf{B}$ is a subset of the row space of $\mathbf{A}$, we have $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{B})$.

  • Indeed, the loss in rank due to multiplication can be quantified as $$ \text{rank}(\mathbf{A} \mathbf{B}) = \text{rank}(\mathbf{B}) - \text{dim}(\mathcal{N}(\mathbf{A}) \cap \mathcal{C}(\mathbf{B})). $$ See BR Theorem 5.4 (p136) for proof.

  • BR Lemma 5.3. $\text{rank}(\mathbf{A}\mathbf{B}) = \text{rank}(\mathbf{A})$ if $\mathbf{B}$ is square and of full rank. More general, left-multiplying by a matrix with full column rank or right-multiplying by a matrix of full row rank does not change rank.

    Proof: We show the more general statement. Assume $\mathbf{B} \in \mathbb{R}^{m \times n}$ has full row rank, we want to show $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{B})$. Since $\mathbf{B} \in \mathbb{R}^{m \times n}$ has full row rank, there exists a permutation matrix $\mathbf{P} \in \{0,1\}^{n \times n}$ such that $$ \mathbf{B} \mathbf{P} = \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix}, $$ where $\mathbf{B}_1 \in \mathbb{R}^{m \times m}$ is non-singular and $\mathbf{B} \in \mathbb{R}^{m \times (n-m)}$. Then $$ \text{rank}(\mathbf{A}) \ge \text{rank}(\mathbf{A}\mathbf{B}) = \text{rank}(\mathbf{A} \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix} \mathbf{P}') \ge \text{rank} \left( \mathbf{A} \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix} \mathbf{P}' \mathbf{P} \begin{pmatrix} \mathbf{B}_1^{-1} \\ \mathbf{O} \end{pmatrix} \right) = \text{rank} (\mathbf{A} \mathbf{I}_n) = \text{rank} (\mathbf{A}). $$ Thus $\text{rank}(\mathbf{A}) = \text{rank} (\mathbf{A} \mathbf{B})$. Proof for the other half of the statement follows the same argument.

  • Example: 2019 qual. exam Q1.

Nullity

  • The nullity of a matrix $\mathbf{A}$ is the dimension of its null space $$ \text{nullity}(\mathbf{A}) = \text{dim}(\mathcal{N}(\mathbf{A})). $$

  • If $\mathcal{N}(\mathbf{A}) \subseteq \mathcal{N}(\mathbf{B})$, then $\text{rank}(\mathbf{A}) \ge \text{rank}(\mathbf{B})$.

    Proof: If $\mathbf{A} \mathbf{x} = \mathbf{0}$, then $\mathbf{B} \mathbf{x} = \mathbf{0}$. Then for any set of linearly independent columns in $\mathbf{B}$, the corresponding columns in $\mathbf{A}$ are linearly independent as well. Thus the maximum number of linearly independent columns in $\mathbf{A}$ is at least as many as that of $\mathbf{B}$.

  • BR Lemma 5.1. $\text{nullity}(\mathbf{A}) \le \text{nullity}(\mathbf{B} \mathbf{A})$. (Left) matrix multiplication can only inreases the nullity.

    Proof: Since $\mathcal{N}(\mathbf{A}) \subseteq \mathcal{N}(\mathbf{B} \mathbf{A})$ (why?), we have $\text{nullity}(\mathbf{A}) \le \text{nullity}(\mathbf{B} \mathbf{A})$.

Rank-nullity theorem

  • BR Theorem 5.1. Let $\mathbf{A} \in \mathbb{R}^{m \times n}$, then $$ \text{rank}(\mathbf{A}) + \text{nullity}(\mathbf{A}) = n. $$

    Proof: Denote $\nu = \text{nullity}(\mathbf{A}) = \text{dim}(\mathcal{N}(\mathbf{A}))$. Let $\mathbf{X} \in \mathbb{R}^{n \times n}$ be $$ \mathbf{X} = \begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix}, $$ where columns of $\mathbf{X}_1 \in \mathbb{R}^{n \times \nu}$ form a basis of $\mathcal{N}(\mathbf{A})$ and columns of $\mathbf{X}_2 \in \mathbb{R}^{n \times (n - \nu)}$ extend those in $\mathbf{X}_1$ to be a basis of $\mathbb{R}^n$. We show columns of $\mathbf{A} \mathbf{X}_2$ form a basis of $\mathcal{C}(\mathbf{A})$. Thus $\text{rank}(\mathbf{A}) = \text{dim}(\mathcal{C}(\mathbf{A})) = n - \nu$.
    (1) To show that columns of $\mathbf{A} \mathbf{X}_2$ are linearly independent. Assume $\mathbf{A} \mathbf{X}_2 \mathbf{v} = \mathbf{0}$. Then $\mathbf{X}_2 \mathbf{v} \in \mathcal{N}(\mathbf{A}) = \mathcal{C}(\mathbf{X}_1)$. Thus $\mathbf{X}_2 \mathbf{v} = \mathbf{X}_1 \mathbf{u}$ for some $\mathbf{u}$, or equivalently, $$ \begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix} \begin{pmatrix} -\mathbf{u} \\ \mathbf{v} \end{pmatrix} = \mathbf{0}_n. $$ Since the matrix $\begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix}$ is non-singular, we must have $\mathbf{u}=\mathbf{0}$ and $\mathbf{v}=\mathbf{0}$. This shows that $\mathbf{v}=\mathbf{0}$ whenever $\mathbf{A} \mathbf{X}_2 \mathbf{v} = \mathbf{0}$. So the columns of $\mathbf{A} \mathbf{X}_2$ is linearly independent.
    (2) Next we show the columns of $\mathbf{A} \mathbf{X}_2$ span $\mathcal{C}(\mathbf{A})$ by showing $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \subseteq \mathcal{C}(\mathbf{A})$ and $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \supseteq \mathcal{C}(\mathbf{A})$. One direction $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \subseteq \mathcal{C}(\mathbf{A})$ is easy. To show the other direction $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{A} \mathbf{X}_2)$, let $\mathbf{w} \in \mathcal{C}(\mathbf{A})$. Then $\mathbf{w} = \mathbf{A} \mathbf{y}$ for some vector $\mathbf{y}$. Because $\mathbf{y} \in \mathbb{R}^n$, which is spanned by columns of $\mathbf{X}$, we can write $\mathbf{y} = \mathbf{X}_1 \mathbf{z}_1 + \mathbf{X}_2 \mathbf{z}_2$ for some vectors $\mathbf{z}_1$ and $\mathbf{z}_2$. Thus $\mathbf{w} = \mathbf{A} \mathbf{X}_1 \mathbf{z}_1 + \mathbf{A} \mathbf{X}_2 \mathbf{z}_2 = \mathbf{A} \mathbf{X}_2 \mathbf{z}_2 \in \mathcal{C}(\mathbf{A} \mathbf{X}_2)$. This proves $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{A} \mathbf{X}_2)$.

Fundamental theorem of ranks

  • BR Theorem 5.2. $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}') = \text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{A}')$.

    Proof: $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}')$ by definition of rank (row rank = column rank = rank). Early on we showed $\mathcal{N}(\mathbf{A}'\mathbf{A}) = \mathcal{N}(\mathbf{A})$. Thus $\text{nullity}(\mathbf{A}) = \text{nullity}(\mathbf{A}'\mathbf{A})$. Then by the rank-nullity theorem, $\text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A})$.

  • Matrices of form $\mathbf{A}'\mathbf{A}$ or $\mathbf{A}\mathbf{A}'$ are called the Gram matrix or Gramian matrix.

Rank factorization

  • Let $\mathbf{A} \in \mathbb{R}^{m \times n}$ with rank $r \ge 1$. The product $\mathbf{A} = \mathbf{C} \mathbf{R}$, where $\mathbf{C} \in \mathbb{R}^{m \times r}$ and $\mathbf{R} \in \mathbb{R}^{r \times n}$ is called a rank decomposition or rank factorization of $\mathbf{A}$.

  • Visualize: TODO.

  • Existence of rank factorization. Any non-null matrix has a rank decomposition. To construct one, let columns of \begin{eqnarray*} \mathbf{C} = \begin{pmatrix} \mid & & \mid \\ \mathbf{c}_1 & \cdots & \mathbf{c}_r \\ \mid & & \mid \end{pmatrix} \end{eqnarray*} be a basis of $\mathcal{C}(\mathbf{A})$. Then $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{C})$. Thus there exists $\mathbf{R}$ such that $\mathbf{A} = \mathbf{C} \mathbf{R}$.

  • Is rank factorization unique? $\mathbf{A} = \mathbf{C} \mathbf{R} = (\mathbf{C} \mathbf{M}) (\mathbf{M}^{-1} \mathbf{R})$ for any non-singular matrix $\mathbf{M}^{r \times r}$.

  • (Skip) Given a rank factorization $\mathbf{A} = \mathbf{C} \mathbf{R}$, $$ \text{rank}(\mathbf{A}') = \text{rank}(\mathbf{R}' \mathbf{C}') \le \text{rank}(\mathbf{R}') \le r = \text{rank}(\mathbf{A}). $$ Now apply the same argument to rank factorization $\mathbf{A}' = \mathbf{R}' \mathbf{C}'$, we get the other direction $$ \text{rank}(\mathbf{A}) \le \text{rank}(\mathbf{A}'). $$ Thus we have an alternative proof of the result $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}')$.

  • If $\mathbf{A} \in \mathbb{R}^{m \times n}$ with rank $r$ can be factorized as $\mathbf{A} = \mathbf{U} \mathbf{V}$, where $\mathbf{U} \in \mathbb{R}^{m \times k}$ and $\mathbf{V} \in \mathbb{R}^{k \times n}$, then $k \ge r$.

    Proof: Since $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{U}\mathbf{V}) \subseteq \mathcal{C}(\mathbf{U})$, $r = \text{rank}(\mathbf{A}) \le \text{rank}(\mathbf{U}) \le k$.

  • Let $\text{rank}(\mathbf{A}) = r$ and $\mathbf{A} = \mathbf{C} \mathbf{R}$ be a rank factorization. Then

    1. $\text{rank}(\mathbf{C}) = \text{rank}(\mathbf{R}) = r$,

    2. $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{C})$, $\mathcal{C}(\mathbf{A}') = \mathcal{C}(\mathbf{R}')$ and $\mathcal{N}(\mathbf{A}) = \mathcal{N}(\mathbf{R})$.

      Proof of 1: $r = \text{rank}(\mathbf{A}) = \text{rank}(\mathbf{C}\mathbf{R}) \le \text{rank}(\mathbf{C}) \le r$. Thus $\text{rank}(\mathbf{C}) = r$. Similarly $\text{rank}(\mathbf{R}) = r$.
      Proof of 2: $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{C})$ is trivial. Suppose $\mathcal{C}(\mathbf{C})$ is strictly larger than $\mathcal{C}(\mathbf{A})$. Then there exists vector $\mathbf{v} \in \mathcal{C}(\mathbf{C})$ that is not a linear combination of columns of $\mathbf{A}$. Let $\mathbf{u}_1, \ldots, \mathbf{u}_r$ be a basis of $\mathcal{C}(\mathbf{A})$. Then the $r+1$ vectors $\mathbf{u}_1, \ldots, \mathbf{u}_r, \mathbf{v}$ is an independent set in $\mathcal{C}(\mathbf{C})$, contadicting the fact $\text{rank}(\mathbf{C}) = r$. Therefore we must have $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{C})$. Similar argument shows $\mathcal{C}(\mathbf{A}') = \mathcal{C}(\mathbf{R}')$.
      To show $\mathcal{N}(\mathbf{A}) = \mathcal{N}(\mathbf{R})$, one direction $\mathcal{N}(\mathbf{A}) \supseteq \mathcal{N}(\mathbf{R})$ is trivial (why?). To show the other direction, \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}) \\ &\Rightarrow& \mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{C} \mathbf{R} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{R} \mathbf{x} \in \mathcal{N}(\mathbf{C}). \end{eqnarray*} But by the rank-nullity theorem, $\text{nullity}(\mathbf{C}) = r - \text{rank}(\mathbf{C}) = 0$. Thus $\mathbf{R} \mathbf{x} = \mathbf{0}$, that is $\mathbf{x} \in \mathcal{N}(\mathbf{R})$. We have shown $\mathcal{N}(\mathbf{A}) \subseteq \mathcal{N}(\mathbf{R})$.

Rank of a partitioned matrix

  • BR Theorem 5.11. $$ \text{rank} \begin{pmatrix} \mathbf{A}_{11} & \mathbf{0} \\ \mathbf{0} & \mathbf{A}_{22} \end{pmatrix} = \text{rank}(\mathbf{A}_{11}) + \text{rank}(\mathbf{A}_{22}). $$

    Proof: It is easy to see for any independent columns in $\begin{pmatrix} \mathbf{A}_{11} & \mathbf{0} \\ \mathbf{0} & \mathbf{A}_{22} \end{pmatrix}$, the corresponding columns in first $n_1$ and second $n_2$ positions are independent as well.

  • BR Theorem 5.12. Let $$ \mathbf{A} = \begin{pmatrix} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{pmatrix} $$ be a $2 \times 2$ partitioned matrix.

    1. If $\mathbf{A}_{11}$ is non-singular, then $$ \text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}_{11}) + \text{rank}(\mathbf{A}_{22} - \mathbf{A}_{21} \mathbf{A}_{11}^{-1} \mathbf{A}_{12}). $$

    2. If $\mathbf{A}_{22}$ is non-singular, then $$ \text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}_{22}) + \text{rank}(\mathbf{A}_{11} - \mathbf{A}_{12} \mathbf{A}_{22}^{-1} \mathbf{A}_{21}). $$

      Proof: The key is the identity $$ \begin{pmatrix} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{pmatrix} = \begin{pmatrix} \mathbf{I}_{n_1} & \mathbf{0} \\ \mathbf{A}_{21} \mathbf{A}_{11}^{-1} & \mathbf{I}_{n_2} \end{pmatrix} \begin{pmatrix} \mathbf{A}_{11} & \mathbf{0} \\ \mathbf{0} & \mathbf{A}_{22} - \mathbf{A}_{21} \mathbf{A}_{11}^{-1} \mathbf{A}_{12} \end{pmatrix} \begin{pmatrix} \mathbf{I}_{n_1} & \mathbf{A}_{11}^{-1} \mathbf{A}_{12} \\ \mathbf{0} & \mathbf{I}_{n_2} \end{pmatrix}, $$ which is direclty verified by multiplying the matrices on the right hand side. Since pre- and post-multiplying by a nonsingular matrix does not change rank, we have $$ \text{rank}(\mathbf{A}) = \text{rank} \begin{pmatrix} \mathbf{A}_{11} & \mathbf{0} \\ \mathbf{0} & \mathbf{A}_{22} - \mathbf{A}_{21} \mathbf{A}_{11}^{-1} \mathbf{A}_{12} \end{pmatrix} = \text{rank}(\mathbf{A}_{11}) + \text{rank}(\mathbf{A}_{22} - \mathbf{A}_{21} \mathbf{A}_{11}^{-1} \mathbf{A}_{12}). $$ The second part is proved in a similar way.