Vector space (BR Chapter 4)¶

Vector space¶

A vector space or linear space or linear subspace or subspace $\mathcal{S} \subseteq \mathbb{R}^n$ is a set of vectors in $\mathbb{R}^n$ that are closed under addition and scalar multiplication. In other words, $\mathcal{S}$ must satisfy
1. If $\mathbf{x}, \mathbf{y} \in \mathcal{S}$, then $\mathbf{x} + \mathbf{y} \in \mathcal{S}$.
2. If $\mathbf{x} \in \mathcal{S}$, then $\alpha \mathbf{x} \in \mathcal{S}$ for any $\alpha \in \mathbb{R}$.
  Or equivalently the set is closed under axpy operation. $\alpha \mathbf{x} + \mathbf{y} \in \mathcal{S}$ for all $\mathbf{x}, \mathbf{y} \in \mathcal{S}$ and $\alpha \in \mathbb{R}$.

# TODO vector diagram for addition and scalar multiplication

Any vector space must contain the zero vector $\mathbf{0}$ (why?).
Examples of vector space:
- Origin: $\{\mathbf{0}\}$.
- Line passing origin: $\{\alpha \mathbf{x}: \alpha \in \mathbb{R}\}$ for a fixed vector $\mathbf{x} \in \mathbb{R}^n$.
- Plane passing origin: $\{\alpha_1 \mathbf{x}_1 + \alpha_2 \mathbf{x}_2: \alpha_1, \alpha_2 \in \mathbb{R}\}$ for two fixed vectors $\mathbf{x}_1, \mathbf{x}_2 \in \mathbb{R}^n$.
- Euclidean space: $\mathbb{R}^n$.
Order and dimension. The order of a vector space is simply the length of the vectors in that space. Not to be confused with the dimension of a vector space, which we later define as the maximum number of linearly independent vectors in that space.
BR Theorem 4.2. If $\mathcal{S}_1$ and $\mathcal{S}_2$ are two vector spaces of same order, then their intersection $\mathcal{S}_1 \cap \mathcal{S}_2$ is a vector space.

Proof: Let $\mathbf{x}, \mathbf{y}$ be two arbitrary vectors in $\mathcal{S}_1 \cap \mathcal{S}_2$ and $\alpha \in \mathbb{R}$. Then $\alpha \mathbf{x} + \mathbf{y} \in \mathcal{S}_1$ because $\mathbf{x}, \mathbf{y} \in \mathcal{S}_1$ and $\mathcal{S}_1$ is a vector space. Similarly $\alpha \mathbf{x} + \mathbf{y} \in \mathcal{S}_2$. Therefore $\alpha \mathbf{x} + \mathbf{y} \in \mathcal{S}_1 \cap \mathcal{S}_2$.
Two vector spaces $\mathcal{S}_1$ and $\mathcal{S}_2$ are essentially disjoint or virtually disjoint if the only element in $\mathcal{S}_1 \cap \mathcal{S}_2$ is the zero vector $\mathbf{0}$.
If $\mathcal{S}_1$ and $\mathcal{S}_2$ are two vector spaces of same order, then their union $\mathcal{S}_1 \cup \mathcal{S}_2$ is not necessarily a vector space.

TODO: Give a counter example.
BR Theorem 4.3. Define the sum of two vector spaces $\mathcal{S}_1$ and $\mathcal{S}_2$ of same order by $$ \mathcal{S}_1 + \mathcal{S}_2 = \{\mathbf{x}_1 + \mathbf{x}_2: \mathbf{x}_1 \in \mathcal{S}_1, \mathbf{x}_2 \in \mathcal{S}_2\}. $$ Then $\mathcal{S}_1 + \mathcal{S}_2$ is the smallest vector space that contains $\mathcal{S}_1 \cup \mathcal{S}_2$.

Proof: Let $\mathbf{u}, \mathbf{v} \in \mathcal{S}_1 + \mathcal{S}_2$ and $\alpha \in \mathbb{R}$, we want to show $\alpha \mathbf{u} + \mathbf{v} \in \mathcal{S}_1 + \mathcal{S}_2$. Write $\mathbf{u} = \mathbf{x}_1 + \mathbf{x}_2$ and $\mathbf{v} = \mathbf{y}_1 + \mathbf{y}_2$, where $\mathbf{x}_1, \mathbf{y}_1 \in \mathcal{S}_1$ and $\mathbf{x}_2, \mathbf{y}_2 \in \mathcal{S}_2$, then $$ \alpha \mathbf{u} + \mathbf{v} = (\alpha \mathbf{x}_1 + \alpha \mathbf{x}_2) + (\mathbf{y}_1 + \mathbf{y}_2) = (\alpha \mathbf{x}_1 + \mathbf{y}_1) + (\alpha \mathbf{x}_2 + \mathbf{y}_2) \in \mathcal{S}_1 + \mathcal{S}_2. $$ Thus $\mathcal{S}_1 + \mathcal{S}_2$ is a vector space.
To show $\mathcal{S}_1 + \mathcal{S}_2$ is the smallest vector space containing $\mathcal{S}_1 \cup \mathcal{S}_2$, let $\mathcal{S}_3$ be a vector space that contains $\mathcal{S}_1 \cup \mathcal{S}_2$. We will show $\mathcal{S}_3$ must contain $\mathcal{S}_1 + \mathcal{S}_2$. Let $\mathbf{u} \in \mathcal{S}_1 + \mathcal{S}_2$ so $\mathbf{u} = \mathbf{x} + \mathbf{y}$, where $\mathbf{x} \in \mathcal{S}_1$ and $\mathbf{y} \in \mathcal{S}_2$. Since both $\mathbf{x}$ and $\mathbf{y}$ belong to $\mathcal{S}_1 \cup \mathcal{S}_2 \subseteq \mathcal{S}_3$. So $\mathbf{u} = \mathbf{x} + \mathbf{y} \in \mathcal{S}_3$.
Example: Let $\mathcal{S}_1$ and $\mathcal{S}_2$ be two lines in $\mathbb{R}^2$ that passes the origin and not parallel to each other. What are $\mathcal{S}_1 \cap \mathcal{S}_2$ and $\mathcal{S}_1 + \mathcal{S}_2$?

Affine space (optional)¶

Consider a system of $m$ linear equations in variable $\mathbf{x} \in \mathbb{R}^n$ \begin{eqnarray*} \mathbf{c}_1' \mathbf{x} &=& b_1 \\ \vdots &=& \vdots \\ \mathbf{c}_m' \mathbf{x} &=& b_m, \end{eqnarray*} where $\mathbf{c}_1,\ldots,\mathbf{c}_m \in \mathbb{R}^n$ are linearly independent (and hence $m \le n$). The set of solutions is called an affine space.
The intersection of two affine spaces is an affine space (why?). If the zero vector $\mathbf{0}$ belongs to the affine space, i.e., $b_1=\cdots=b_m=0$, then it is a vector space. Thus any affine space containing the origin $\mathbf{0}$ is a vector space, but other affine spaces are not vector spaces.
If $m=1$, the affine space is called a hyperplane. A hyperplane through the origin is an $(n-1)$-dimensional vector space.
If $m=n-1$, the affine space is a line. A line through the origin is a one-dimensional vector space.
The mapping $\mathbf{x} \mapsto \mathbf{A} \mathbf{x} + \mathbf{b}$ is called an affine function. If $\mathbf{b} = \mathbf{0}$, it is called a linear function.

Span¶

The span of a set of $\mathbf{x}_1,\ldots,\mathbf{x}_n \in \mathbb{R}^m$, defined as the set of all possible linear combinations of $\mathbf{x}_i$s $$ \text{span} \{\mathbf{x}_1,\ldots,\mathbf{x}_n\} = \left\{\sum_{i=1}^n \alpha_i \mathbf{x}_i: \alpha_i \in \mathbb{R} \right\}, $$ is a vector space in $\mathbb{R}^m$.

Proof: TODO

Four fundamental subspaces¶

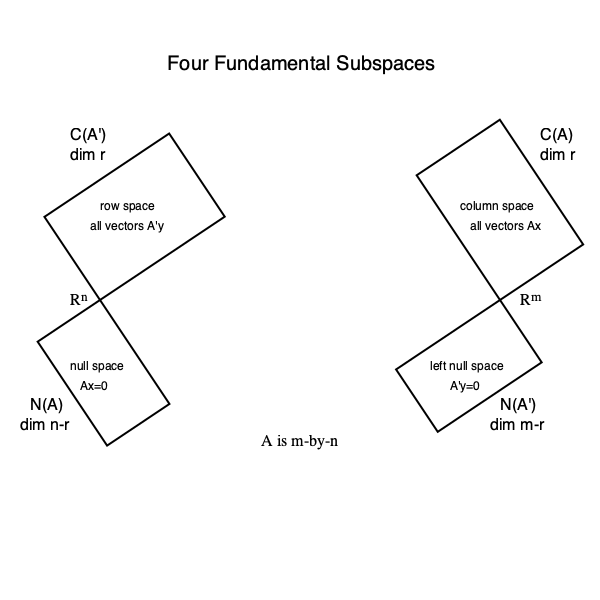
Let $\mathbf{A}$ be an $m \times n$ matrix \begin{eqnarray*} \mathbf{A} = \begin{pmatrix} \mid & & \mid \\ \mathbf{a}_1 & \ldots & \mathbf{a}_n \\ \mid & & \mid \end{pmatrix}. \end{eqnarray*}

The column space of $\mathbf{A}$ is \begin{eqnarray*} \mathcal{C}(\mathbf{A}) &=& \{ \mathbf{y} \in \mathbb{R}^m: \mathbf{y} = \mathbf{A} \mathbf{x} \text{ for some } \mathbf{x} \in \mathbb{R}^n \} \\ &=& \text{span}\{\mathbf{a}_1, \ldots, \mathbf{a}_n\}. \end{eqnarray*} Sometimes it is also called the image or range or manifold of $\mathbf{A}$.
The row space of $\mathbf{A}$ is \begin{eqnarray*} \mathcal{R}(\mathbf{A}) &=& \mathcal{C}(\mathbf{A}') \\ &=& \{ \mathbf{y} \in \mathbb{R}^n: \mathbf{y} = \mathbf{A}' \mathbf{x} \text{ for some } \mathbf{x} \in \mathbb{R}^m \}. \end{eqnarray*}
The null space or kernel of $\mathbf{A}$ is \begin{eqnarray*} \mathcal{N}(\mathbf{A}) = \{\mathbf{x} \in \mathbb{R}^n: \mathbf{A} \mathbf{x} = \mathbf{0}\}. \end{eqnarray*}
The left null space $\mathbf{A}$ is \begin{eqnarray*} \mathcal{N}(\mathbf{A}') = \{\mathbf{x} \in \mathbb{R}^m: \mathbf{A}' \mathbf{x} = \mathbf{0}\}. \end{eqnarray*}

TODO: show these 4 sets are vector spaces.

Example: Draw the four subspaces of matrix $\mathbf{A} = \begin{pmatrix} 1 & -2 & -2 \\ 3 & -6 & -6 \end{pmatrix}$. TODO
Example: Interpret the four subspaces of the incidence matrix of a directed graph. TODO

Effects of matrix multiplication on column/row space¶

BR Theorem 4.6. $\mathcal{C}(\mathbf{C}) \subseteq \mathcal{C}(\mathbf{A})$ if and only if $\mathbf{C} = \mathbf{A} \mathbf{B}$ for some matrix $\mathbf{B}$.

Proof: The if part is easily verified since each column of $\mathbf{C}$ is a linear combination of columns of $\mathbf{A}$. For the only if part, assuming $\mathcal{C}(\mathbf{C}) \subseteq \mathcal{C}(\mathbf{A})$, each column of $\mathbf{C}$ is a linear combination of columns of $\mathbf{A}$. In other words $\mathbf{c}_j = \mathbf{A} \mathbf{b}_j$ for some $\mathbf{b}_j$. Therefore $\mathbf{C} = \mathbf{A} \mathbf{B}$, where $\mathbf{B}$ has columns $\mathbf{b}_j$.
BR Theorem 4.7. $\mathcal{R}(\mathbf{C}) \subseteq \mathcal{C}(\mathbf{A})$ if and only if $\mathbf{C} = \mathbf{B} \mathbf{A}$ for some matrix $\mathbf{B}$.

Proof is similar to that for BR Theorem 4.6.
BR Theorem 4.8. $\mathcal{N}(\mathbf{B}) \subseteq \mathcal{N}(\mathbf{A} \mathbf{B})$.

Proof. For any $\mathbf{x} \in \mathcal{N}(\mathbf{B})$, $\mathbf{A} \mathbf{B} \mathbf{x} = \mathbf{A} (\mathbf{B} \mathbf{x}) = \mathbf{A} \mathbf{0} = \mathbf{0}$. Thus $\mathbf{x} \in \mathcal{N}(\mathbf{A} \mathbf{B})$.

Essential disjointness of four fundamental subspaces¶

BR Theorem 4.11. Row space and null space of a matrix are essentially disjoint. For any matrix $\mathbf{A}$, $$ \mathcal{R}(\mathbf{A}) \cap \mathcal{N}(\mathbf{A}) = \{\mathbf{0}\}. $$

Proof: If $\mathbf{x} \in \mathcal{R}(\mathbf{A}) \cap \mathcal{N}(\mathbf{A})$, then $\mathbf{x} = \mathbf{A}' \mathbf{u}$ for some $\mathbf{u}$ and $\mathbf{A} \mathbf{x} = \mathbf{0}$. Thus $\mathbf{x}' \mathbf{x} = \mathbf{u}' \mathbf{A} \mathbf{x} = \mathbf{u}' \mathbf{0} = 0$, which implies $\mathbf{x} = \mathbf{0}$. This shows $\mathcal{R}(\mathbf{A}) \cap \mathcal{N}(\mathbf{A}) \subseteq \{\mathbf{0}\}$. The other direction is trivial.
Column space and left null space of a matrix are essentially disjoint. For any matrix $\mathbf{A}$, $$ \mathcal{C}(\mathbf{A}) \cap \mathcal{N}(\mathbf{A}') = \{\mathbf{0}\}. $$

Proof: Apply above result to $\mathbf{A}'$.
BR Theorem 4.12. \begin{eqnarray*} \mathcal{N}(\mathbf{A}'\mathbf{A}) &=& \mathcal{N}(\mathbf{A}) \\ \mathcal{N}(\mathbf{A}\mathbf{A}') &=& \mathcal{N}(\mathbf{A}'). \end{eqnarray*}

Proof: For the first equation, we note \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}) \\ &\Rightarrow& \mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{A}'\mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{x} \in \mathcal{N}(\mathbf{A}'\mathbf{A}). \end{eqnarray*} This shows $\mathcal{N}(\mathbf{A}) \subseteq \mathcal{N}(\mathbf{A}'\mathbf{A})$. To show the other direction $\mathcal{N}(\mathbf{A}) \supseteq \mathcal{N}(\mathbf{A}'\mathbf{A})$, we note \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}'\mathbf{A}) \\ &\Rightarrow& \mathbf{A}'\mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{x}' \mathbf{A}' \mathbf{A} \mathbf{x} = 0 \\ &\Rightarrow& \|\mathbf{A} \mathbf{x}\|^2 = 0 \\ &\Rightarrow& \mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{x} \in \mathcal{N}(\mathbf{A}). \end{eqnarray*}

For the second equation, we apply the first equation to $\mathbf{B} = \mathbf{A}'$.

(skip) Column/row space of a partitioned matrix¶

BR Theorem 4.9.
1. Assuming $\mathbf{A}$ and $\mathbf{B}$ have same number of rows, $$ \mathcal{C}((\mathbf{A} : \mathbf{B})) = \mathcal{C}(\mathbf{A}) + \mathcal{C}(\mathbf{B}). $$
2. Assuming $\mathbf{A}$ and $\mathbf{C}$ have same number of columns, $$ \mathcal{R} \left( \begin{pmatrix} \mathbf{A} \\ \mathbf{C} \end{pmatrix} \right) = \mathcal{R}(\mathbf{A}) + \mathcal{R}(\mathbf{C}) $$ and $$ \mathcal{N} \left( \begin{pmatrix} \mathbf{A} \\ \mathbf{C} \end{pmatrix} \right) = \mathcal{N}(\mathbf{A}) \cap \mathcal{N}(\mathbf{C}). $$
  
  Proof: To show part 1, we note \begin{eqnarray*} & & \mathbf{x} \in \mathcal{C}((\mathbf{A} : \mathbf{B})) \\ &\Leftrightarrow& \mathbf{x} = \mathbf{A} \mathbf{u} + \mathbf{B} \mathbf{v} \text{ for some } \mathbf{u} \text{ and } \mathbf{v} \\ &\Leftrightarrow& \mathbf{x} \in \mathcal{C}(\mathbf{A}) + \mathcal{C}(\mathbf{B}). \end{eqnarray*}
  To show part 2, we apply part 1 to the transpose.

Linear independence and basis¶

A set of vectors $\mathbf{x}_1, \ldots, \mathbf{x}_n \in \mathbb{R}^m$ are linearly dependent if there exists coefficients $c_j$ such that $\sum_{j=1}^n c_j \mathbf{x}_j = \mathbf{0}$ and $c_j$ are not all 0.

They are linearly independent if $\sum_{j=1}^n c_j \mathbf{x}_j = \mathbf{0}$ implies $c_j=0$ for all $j$.
No linearly independent set can contain the zero vector $\mathbf{0}$. (why?)
A set of linearly independent vectors that span a vector space $\mathcal{S}$ is called a basis of ${\cal S}$.
BR Lemma 4.5. Let $\mathcal{A} = \{\mathbf{a}_1, \ldots, \mathbf{a}_n\}$ be a basis of a vector space $\mathcal{S}$. Then any vector $\mathbf{x} \in \mathcal{S}$ can be expressed uniquely as a linear combination of vectors in $\mathcal{A}$.

Proof: Suppose $\mathbf{x}$ can be expressed by two linear combinations $$ \mathbf{x} = \alpha_1 \mathbf{a}_1 + \cdots + \alpha_n \mathbf{a}_n = \beta_1 \mathbf{a}_1 + \cdots + \beta_n \mathbf{a}_n. $$ Then $(\alpha_1 - \beta_1) \mathbf{a}_1 + \cdots (\alpha_n - \beta_n) \mathbf{a}_n = \mathbf{0}$. Since $\mathbf{a}_i$ are linearly independent, we have $\alpha_i = \beta_i$ for all $i$.
Independence-dimension inequality or order-dimension inequality. If the vectors $\mathbf{x}_1, \ldots, \mathbf{x}_k \in \mathbb{R}^n$ are linearly independent, then $k \le n$.

Proof: We show this by induction. Let $a_1, \ldots, a_k \in \mathbb{R}^1$ be linearly independent. We must have $a_1 \ne 0$. This means that every element $a_i$ of the collection can be expressed as a multiple of $a_i = (a_i / a_1) a_1$ of the first element $a_1$. This contradicts the linear independence thus $k$ must be 1.
Induction hypothesis: suppose $n \ge 2$ and the independence-dimension inequality holds for $k \le n$. We partition the vectors $\mathbf{a}_i \in \mathbb{R}^n$ as $$ \mathbf{a}_i = \begin{pmatrix} \mathbf{b}_i \\ \alpha_i \end{pmatrix}, \quad i = 1,\ldots,k, $$ where $\mathbf{b}_i \in \mathbb{R}^{n-1}$ and $\alpha_i \in \mathbb{R}$.
First suppose $\alpha_1 = \cdots = \alpha_k = 0$. Then the vectors $\mathbf{b}_1, \ldots, \mathbf{b}_k$ are linearly independent: $\sum_{i=1}^k \beta_i \mathbf{b}_i = \mathbf{0}$ if and only if $\sum_{i=1}^k \beta_i \mathbf{a}_i = \mathbf{0}$, which is only possible for $\beta_1 = \cdots = \beta_k = 0$ because the vectors $\mathbf{a}_i$ are linearly independent. The vectors $\mathbf{b}_i$ therefore form a linearly independent collection of $(n-1)$-vectors. By the induction hypothesis we have $k \le n-1$ so $k \le n$.
Next we assume the scalars $\alpha_i$ are not all zero. Assume $\alpha_j \ne 0$. We define a collection of $k-1$ vectors $\mathbf{c}_i$ of length $n-1$ as follows: $$ \mathbf{c}_i = \mathbf{b}_i - \frac{\alpha_i}{\alpha_j} \mathbf{b}_j, \quad i = 1, \ldots, j-1, \mathbf{c}_i = \mathbf{b}_{i+1} - \frac{\alpha_{i+1}}{\alpha_j} \mathbf{b}_j, \quad i = j, \ldots, k-1. $$ These $k-1$ vectors are linealy independent: If $\sum_{i=1}^{k-1} \beta_i c_i = 0$ then $$ \sum_{i=1}^{j-1} \beta_i \begin{pmatrix} \mathbf{b}_i \\ \alpha_i \end{pmatrix} + \gamma \begin{pmatrix} \mathbf{b}_j \\ \alpha_j \end{pmatrix} + \sum_{i=j+1}^k \beta_{i-1} \begin{pmatrix} \mathbf{b}_i \\ \alpha_i \end{pmatrix} = \mathbf{0} $$ with $\gamma = - \alpha_j^{-1} \left( \sum_{i=1}^{j-1} \beta_i \alpha_i + \sum_{i=j+1}^k \beta_{i-1} \alpha_i \right)$. Since the vectors $\mathbf{a}_i$ are linearly independent, all coefficients $\beta_i$ and $\gamma$ are all zero. This in turns implies that the vectors $\mathbf{c}_1, \ldots, \mathbf{c}_{k-1}$ are linearly independent. By the induction hypothesis $k-1 \le n-1$, we have established $k \le n$.
If $\mathcal{A}=\{\mathbf{a}_1, \ldots, \mathbf{a}_k\}$ is a linearly independent set in a vector space $\mathcal{S} \subseteq \mathbb{R}^{m}$ and $\mathcal{B}=\{\mathbf{b}_1, \ldots, \mathbf{b}_l\}$ spans $\mathcal{S}$, then $k \le l$.

Proof. Define two matrices $$ \mathbf{A} = \begin{pmatrix} \mid & & \mid \\ \mathbf{a}_1 & \ldots & \mathbf{a}_k \\ \mid & & \mid \end{pmatrix} \in \mathbb{R}^{m \times k}, \quad \mathbf{B} = \begin{pmatrix} \mid & & \mid \\ \mathbf{b}_1 & \ldots & \mathbf{b}_l \\ \mid & & \mid \end{pmatrix} \in \mathbb{R}^{m \times l}. $$ Since $\mathcal{B}$ spans $\mathcal{S}$, $\mathbf{a}_i = \mathbf{B} \mathbf{c}_i$ for some vector $\mathbf{c}_i \in \mathbb{R}^l$ for $i=1,\ldots,k$. Let $$ \mathbf{C} = \begin{pmatrix} \mid & & \mid \\ \mathbf{c}_1 & \ldots & \mathbf{c}_k \\ \mid & & \mid \end{pmatrix} \in \mathbb{R}^{l \times k}. $$ Then $\mathbf{A} = \mathbf{B} \mathbf{C}$. Since $$ \mathcal{N}(\mathbf{C}) \subseteq \mathcal{N}(\mathbf{A}) = \{\mathbf{0}\}. $$ The only solution to $\mathbf{C} \mathbf{x} = \mathbf{0}_l$ is $\mathbf{0}_k$. In other words, the columns of $\mathbf{C}$ are linearly independent. Thus, by the independence-dimension inequality, $\mathbf{C}$ has at least as many rows as columns. That is $k \le l$.
BR Theorem 4.20. Let $\mathcal{A}=\{\mathbf{a}_1, \ldots, \mathbf{a}_k\}$ and $\mathcal{B}=\{\mathbf{b}_1, \ldots, \mathbf{b}_l\}$ be two basis of a vector space $\mathcal{S}$. Then $k = l$.

Proof: This immediately follows from the previous result.
The dimension of a vector space $\mathcal{S}$, denoted by $\text{dim}(\mathcal{S})$, is defined as
1. the number of vectors in any basis of $\mathcal{S}$, or
2. the maximmal number of linearly independent vectors in $\mathcal{S}$, or
3. the minimal number of vectors that span $\mathcal{S}$.
Monotonicity of dimension. If $\mathcal{S}_1 \subseteq \mathcal{S}_2 \subseteq \mathbb{R}^m$ are two vector spaces of same order, then $\text{dim}(\mathcal{S}_1) \le \text{dim}(\mathcal{S}_2)$.

Proof: Any independent set of vectors in $\mathcal{S}_1$ also live in $\mathcal{S}_2$. Thus the maximal number of independent vectors in $\mathcal{S}_2$ can only be larger or equal to the maximal number of indepedent vectors in $\mathcal{S}_1$.